1. Алгебра
  2. Разложите на множители числитель

Разложите на множители числитель и знаменатель дроби и сократить дробь 9x²-6x+1/6x²+x-1

ауе59 ауе59    1   27.09.2019 08:51    8

Ответы
Evklidushka Evklidushka  08.10.2020 22:21

Разложим на множители числитель с решения уравнения через дискриминант (на самом деле там можно выделить полный квадрат, но через дискриминант надёжнее):

9x^2-6x+1=0\\D=(-6)^2-4 \cdot 9=36-36=0\\x=\dfrac{-b}{2a}=\dfrac{6}{18}=\dfrac{1}{3}\\9x^2-6x+1=9\left(x-\dfrac{1}{3}\right)^2=3^2\left(x-\dfrac{1}{3}\right)^2=(3x-1)^2

Теперь разложим на множители знаменатель:

6x^2+x-1=0\\D=1^2-4 \cdot 6 \cdot (-1)=1+24=25\\\sqrt{D}=5\\x_1=\dfrac{-1+5}{12}=\dfrac{4}{12}=\dfrac{1}{3}\\x_2=\dfrac{-1-5}{12}=\dfrac{-6}{12}=-\dfrac{1}{2}\\6x^2+x-1=6\left(x-\dfrac{1}{3}\right)\left(x+\dfrac{1}{2}\right)=3 \left(x-\dfrac{1}{3}\right) \cdot 2\left(x+\dfrac{1}{2}\right)=\\=(3x-1)(2x+1)

Тогда:

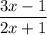\dfrac{9x^2-6x+1}{6x^2+x-1}=\dfrac{(3x-1)^2}{(3x-1)(2x+1)}=\dfrac{3x-1}{2x+1}.

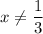ответ: \dfrac{3x-1}{2x+1} при x \neq \dfrac{1}{3}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Иленьк Иленьк  30.10.2020 08:43
6. Высота моста над рекой выражена числом корень 30 м. Сможет ли пройти под этим мостом судно, высота которого над уровнем воды 3,2 м...
Метеор73 Метеор73  30.10.2020 08:43
Расположите в порядке возрастания числа:2√6,√29,3√3. (2б)...
Fin208 Fin208  30.10.2020 08:43
найдите функцию, обратную функции (на фото) запишите область определения полученной функции. за спам бан!​...
martinovvanya2 martinovvanya2  30.10.2020 08:43
Разложите на множители:a) 6 + 8y​...
petrokozlo998 petrokozlo998  30.10.2020 08:44
Разложите на множители: ах²- bx² + ах — bx + 2а - 2b.​...
alaaaaaaa alaaaaaaa  30.10.2020 08:44
Освободитесь от иррациональности в знаменателе дроби:...
wionk wionk  30.10.2020 08:44
Функциясының қасиеттерін төмендегі схема бойынша сипатта...
Duma10 Duma10  30.10.2020 08:44
Решить уравнения1) 2x +3x+1= 02) 9х2 + 6х +1= 0...
Kristiana132435 Kristiana132435  17.05.2020 15:16
Реши систему уравнений методом алгебраического сложения:{t2+y2=61t2−y2=111.{t1=y1=2.{t2=y2=−3.{t3=−y3=4.{t4=−y4=−​...
ГАЛЯ2006261011444 ГАЛЯ2006261011444  07.12.2021 12:05
B) область значений функции y=-2x+5/2 на отрезке -2≤х≤2 очень нужно....

Популярные вопросы