Разложить функцию 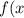=(1+e^{x^2})^{\frac{1}{2}}) по формуле тейлора до
по формуле тейлора до ) при
при  .
.
Другие вопросы по теме Алгебра
Популярные вопросы
- Объясните смысл данных пословиц чему они учат запишите под диктовку...
2 - в теплоизолированном баке с нагревательным элементом заморозили...
2 - с химией. Определите объём 2 граммов газообразного водорода если...
1 - Конспект на тему Культура племен древности нужно ...
3 - Ходить по рыхлому снегу неудобно, так как ноги всегда проваливаются...
3 - Ғарыш кеңістігі мен жұлдыздар ғаламды құрайды. Жұлдыздар бұл...
2 - Доклад ОДНКНР Буддизм в России...
3 - : 9Сколько кубиков в каждой фигуре?2)3)4)ano ROTA-...
3 - 8. Измерь стороны Многоугольников. Вычисли их периметр. e)жВLF3)NGKАС2.оРВьNSRa)D...
2 - Кольцо из проводника подключили к источнику с постоянным напряжением...
3
Рассмотрим и разложим ее по формуле Тейлора до
и разложим ее по формуле Тейлора до  .
.
А тогда искомое разложение