Расстояние между двумя пристанями на реке равно 6 км.катер проплыл это расстояние по течению реки и вернулся обратно 3 часа 45 минут.найдите собственную скорость катера если скорость реки 2 км/ч..буквой x обозначьте собственную скорость катера.
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Трапециянын табаны 6 см және 8 см. Онын орта сызыгын табында2.Трапециянын...
3 - Уақыт - адам өмірінің ақшалай құны. Уақыт-әркімнің өмірлік капиталы....
3 - Первообразнаяf(x)=3x^2-2x M(1;4) ...
2 - Какие цвета использует художник для передачи настроение...
3 - Монитор виды мониторов информатика 5 класс...
2 - Температуры тел можно количественно сравнить с органов чувств???...
3 - Задание 3. С рисунков расскажите о жизни города-комму- ны. Трудно...
1 - расплажи предложения в правильном порядке,чтобы получилься простой...
3 - Са vury vov - Lviv.Көркемдегіш құралдың түрінанықта.Айтпақ ойды,...
3 - растушуйте оксида металичних елементів зі збільшенням їхньої...
2
Пусть собственная скорость катера равна х км/ч, тогда скорость катера по течению реки равна (х+2)км/ч, а против течения реки (х-2)км/ч. Так как расстояние между пристанями равно 6 км, то время с которым катер прыл туда равно 6/(х+2), а обратно 6/(х-2). Тогда
6/(х+2)+6/(х-2)=3,45
v t s
По течению - (х+2) км/ч 6/(х+2) ч 6 км
Против течения - (х-2) км/ч 6/(х-2) ч 6 км
Скорсть течения - 2 км/ч
Собст. скорость - х км/ч
Всего время будет равно 3,75 часа.
Составим и решим уравнение:
24x-48+24x+48-15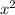 +60=0
+60=0
48x-15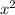 +60=0
+60=0
15x2-48x-60=0
x 4,2
4,2
4,2(км/ч) - собственная скорость катера.
ответ: 4,2 км/ч.
Не уверен, конечно, что правильно. Скорее всего ты ошиблась в написании задания (условия). Перепроверь и реши по-аналогии.