Рассмотрим функцию 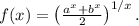Предполагается, что 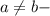положительные числа. Докажите, что f(x) возрастает на всей числовой прямой.
Почему это так важно - дело в том, что f(1) является средним арифметическим чисел a и b, f(2) - средним квадратическим, f(-1) - средним гармоническим, а f(0), если доопределить функцию в нуле по непрерывности, - средним геометрическим.

ромашка261    1   24.07.2021 11:59    1