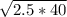
Расскажите подробно как это решается, проспал урок, вот.
Другие вопросы по теме Алгебра
Популярные вопросы
- Что такое пирамида? рассказать о ней....
3 - 37умножить на 2 и 45-17 и 156: 12 31умножить на 7...
2 - Записать три слова с непроверяемыми орфограммами 3 класс...
1 - Сочинить рассказ в мире словосочетаний...
2 - 121 учебник рыбченкова 6 класс вопрос : с каких синонимов можно передать то...
3 - Почему люди не рады северному сиянию...
3 - Определи что значит читать с выражением...
1 - Ученикам 7 класса вопрос как называются сезонные ветры, дующие в северной...
2 - Назовите форму родительного падежа множественного числа существительных женского...
1 - Напишите о пушкине (расцвет тв-ва, взаимоотношения с властью) 5-10 пердложений...
1
В записи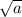 неотрицательное число
неотрицательное число  — подкоренное выражение.
— подкоренное выражение.
Суть квадратного корня: действие, обратное квадрату выражения, то есть для
Примеры:
Если подкоренное выражение арифметического квадратного корня отрицательное, то такого корня не существует!
Задание:
Здесь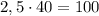 , где
, где 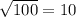 , так как
, так как  и
и 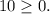
ответ:
10
Объяснение: