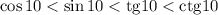Расположите в порядке возрастания числа tg 10; sin 10; cos 10; ctg 10

Ответы

Kotliarrostislav 09.10.2020 05:03

Возьмем приближенно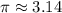 $\pi \approx3.14$

Рассмотрим число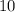 . На числовой окружности этому числу соответствует та же точка, что и числу $10-2\pi$ :

$10-2\pi\approx10-2\cdot3.14=3.72$

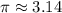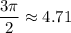Зная, что $\pi \approx3.14$ и $\dfrac{3\pi}{2} \approx4.71$ , получаем, что число 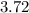3.72 располагается в 3 четверти. Значит, можно сказать о знаках тригонометрических функций: косинус и синус - отрицательный, тангенс и котангенс - положительный. Остается сравнить между собой данные две пары.

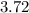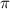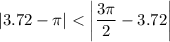Заметим, что число 3.72 располагается ближе к числу $\pi$ , так как $|3.72-\pi|$ .

Зарисуем схематично число в 3 четверти, расположенное ближе к числу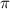 $\pi$ . По рисунку определим, что косинус такого числа (координата х) меньше синуса (координата y):

$\cos10$

Рассмотрим тангенс. Так как тангенс положительный, то заменим отношение синуса к косинусу отношением их модулей:

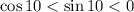$\mathrm{tg}10=\dfrac{\sin10}{\cos10} =\dfrac{|\sin10|}{|\cos10|}$

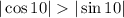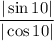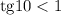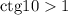Зная, что $\cos10$ , получим, что $|\cos10||\sin10|$ , соответственно дробь $\dfrac{|\sin10|}{|\cos10|}$ правильная, значит $\mathrm{tg}10$ . Тогда, так как котангенс есть величина, обратная тангенсу, то $\mathrm{ctg}101$ .