Пусть x1,x2 - корни квадратного трёхчлена с дискриминантом 1; y1,y2 - корни квадратного трёхчлена с дискриминантом 9; z1,z2 - корни квадратного трёхчлена с дискриминантом d. при каком наименьшем d могло выполняться равенство x1+y1+z1=x2+y2+z2?
Другие вопросы по теме Алгебра
Популярные вопросы
- Что случилось бы если бы не существовало Египтян?...
3 - Гунтина паров одноатомного насыщенного спирта по неоном равна 5,8. Определите...
1 - Найдите формулу соединения, массовая доля никеля в котором 44.6%, а мышьяка 55,4%....
1 - Риси характеру юлько та славко...
2 - Vânătorii fe rațe cuvintele care sunt folosite în formă populară și indicați...
1 - Надрукувати числа від 1 до 10Результатом виконання цієї програми буде стовпчик...
2 - мне сделать контрольную работу по химии...
2 - У яких районах євразії поширені льодовики...
1 - В 1891 году в Хабаровске был построен памятник генерал-губернатору ВосточнойСибири...
3 - Дано температура. Виведіть стан, у якому знаходиться вода при цій температурі(в...
1
4
Объяснение:
Перепишем равенство в другом виде:
Выясним для приведенного уравнения с корнями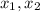 , чему может быть равно выражение
, чему может быть равно выражение  :
:
В зависимости от того, как назначили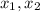 , разность может быть
, разность может быть 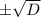 .
.
Пусть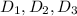 - дискриминанты трех уравнений из условия. Тогда равенство
- дискриминанты трех уравнений из условия. Тогда равенство 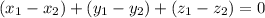 можно будет записать так:
можно будет записать так:
Подставим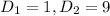 из условия и получим:
из условия и получим:
Но так как значение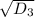 неотрицательно, минимальным значением может быть 2. То есть минимальное
неотрицательно, минимальным значением может быть 2. То есть минимальное 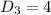 .
.