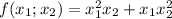Пусть x1 и х2 корни квадратного трехчлена х^2-9х-17.Найдите значение выражения:а)f(x1,x2)=х1^2+х2^2,б)f(x1,x2)=x1^2x2+x1x2^2
Другие вопросы по теме Алгебра
Популярные вопросы
- Жинақтау 1. Жырдағы ең құнды нәрсе не деп ойлайсыңдар?2. «Қыз Жібек» жыры...
1 - Джунгары нападали на аулы казахов в основном ранней___...
3 - Асырма:Сызбанұсқаны дөптерге сызып, өсімдіктер бірлестігінің алмасу себептеринсазындар....
2 - Укажите 3 фактора, влияющие на численость популяции грызунов...
1 - Вказати кількість спільних точок,якщо їх радіуси відповідно =21 см і 33...
2 - В чём особенности движения электрона вокруг ядра...
3 - Инструкции по планированию для кто-то, кто не может пользоваться смартфоном....
3 - Орыс тили 7 сынып 22 упражнение...
2 - Синетика әдісі. Сен өзің қатарлы жеткіншектерге ана тілінің атынан хат...
1 - 1.(1) Яке співвідношення між корисною (Ах) і повною роботою (An) при використанні...
3
1)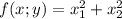
2)