Прямая y=kx+b проходит через точки c(6; 2) и d(-1; -3). найдите k и b и запишите уравнение этой прямой.

Ответы

stazagreen 09.10.2020 20:36

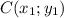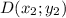Уравнение прямой, проходящей через точки C(x_1; y_1) и D(x_2;y_2) , имеет такой вид:

$\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}$

Подставим в эту формулу известные значения:

$\dfrac{y-2}{-3-2}=\dfrac{x-6}{-1-6}\\\dfrac{y-2}{-5}=\dfrac{x-6}{-7}\\-5(x-6)=-7(y-2)\\5(x-6)=7(y-2)\\5x-30=7y-14\\7y=5x-16\\y=\dfrac{5x-16}{7}\\y=\dfrac{5}{7}x-\dfrac{16}{7}$

$k=\dfrac{5}{7}, \qquad b=-\dfrac{16}{7}.$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

donkikas 14.08.2019 21:00

Решите систему уравнений х-у=3, 2х2+у2=9...

stilist2011 14.08.2019 21:00

Решить 3/4*√169+2*√121/196-(0,2*√6)^2, я уже просто не могу решить это, умоляю....

Ʈгiceгatoρѕ 14.08.2019 21:00

Найти x, если log4 x=-1,5; logx 1/3=-1/2...

SVINKAPIPA 14.08.2019 21:00

Выражения выполняя возведение в степень: ( 1/2 a ^4)3 , ( - 0,4 n^3)2 , ( х ^7/ y^7 ) ^ 3 ,( с^2n)^5 ...

JukovaEleonora 14.08.2019 21:00

Лодка может проплыть расстояние между двумя селениями, стоящими на берегу реки, за 4 часа по течению и за 8 часов против течения. скорость течения реки 2 км/ч. найдите собственную...

missksyushase 14.08.2019 21:00

3x(1-x)²-x²(1-x)=0 решите ,мне для проверки. заранее )....

Dasha112111 14.08.2019 21:00

Вмагазине было 10 розовых пони и 25 солдатиков в первый день продали 20% пони и одна пятая солдатиков сколько всего осталосьв магазине игрушек если за второй день бвло продано 6...

ioiaaea33 18.05.2019 12:30

Запишите девять первых членов последовательности двузначных чисел, кратных числу 6, взятых в порядке убывания....

gigeriti28391vlad 18.05.2019 12:30

Решите неравенств 9-6(4-3x) 24x-15...

круголс 18.05.2019 12:30

1найдите наибольший отрицательный корень уравнения sin^2x=-cos4x 2 выражение cos^4t-sin^4*(t+п) / ctgt-sin2t а) tg t б) 1/cos t в) cos 2t/ sint г) ctg t вас прощу...

Прямая y=kx+b проходит через точки c(6; 2) и d(-1; -3). найдите k и b и запишите уравнение этой прямой.

Популярные вопросы