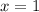Прямая у=8х+4 является касательной к графику функци у= x3+3x2 –x+9. Найти абсциссу точки касания
Другие вопросы по теме Алгебра
Популярные вопросы
- Представьте выражение в виде степени числа х(х 0) или числа а(а...
2 - Устное высказывание. спишите предложения, раскрывая скобки и вставляя...
2 - Определение слова культура (то что человек создаёт)...
1 - Выписать координаты . в заранее...
1 - При обработке 64,2 г. смеси алюминия и оксида алюминия избытком...
3 - Сделать проект по пословицы и поговорки 1)прочитай пословицы и поговорки...
3 - Как соотносятся между собой максимальная сила трения покоя и сила...
1 - Прочти и вычеркни лишние слова.в обычных условиях слон,так же как...
1 - Ilike wendy! 1.he/she is .he/she ).3.he/she is .he/she .he/she ).6.he/she...
2 - Написать сочинение-размышление на тему; путешествуя по россии (что...
3
Поскольку у касательной угловой коэффициент равен 8, то и производная функции в точке касания должна быть равна 8.
Теперь проверим, какая из точек удовлетворяет условие. Для этого достаточно проверить, равны ли значения функции и касательной в каждой конкретной точке.
Функция:
Касательная:
Видим, что в точке с абсциссой 1 функция и касательная принимают одно и то же значение, значит, это и есть искомая точка.
ответ: