1. Алгебра
  2. Производная [tex]y=ctg\sqrt{x}[/tex]

Производная
y=ctg\sqrt{x}

Igarexaaa1 Igarexaaa1    3   09.09.2019 20:55    1

Ответы
Нюта241 Нюта241  16.08.2020 12:55

Это сложная функция. Производная сложной функции:

(f(g(x)))'=f'(g(x))\cdot g'(x)

$(ctg(x))' = -\frac{1}{sin^2x} ; (\sqrt{x} )' = \frac{1}{2\sqrt{x} }

$(ctg(\sqrt{x}))' = -\frac{1}{sin^2(\sqrt{x})} \cdot \frac{1}{2\sqrt{x} }

UPD. Внимательно смотрим на первую формулу. При взятии производной от сложной функции сначала производная берется по "внешней" функции, то есть той, которая вычисляется последней. И вот все то добро, которое у неё в аргументе, никуда не девается.

Формулу можно так записать, чтоб понятнее было:

(f(g(x)))' = f'(t)\cdot t'(x); t=g(x)

То есть это t никуда не девается, поэтому в нашем примере корень остается у квадрата синуса в знаменателе.

Так как это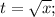 t=\sqrt{x} ;

y = ctg t;

Надеюсь, понятно мысль доложил

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
vasilarina06 vasilarina06  24.04.2020 10:27
решите быстрее, можно поэтапно...
dimanichaev799 dimanichaev799  24.04.2020 10:27
Прямая у=kx+b проходит через точку m (3;1) и е (1;5). запишите уравнение этой прямой​...
Kate24512 Kate24512  24.04.2020 10:27
16х4 – 1 = 0. Решите уравнение ....
vladysh205 vladysh205  24.04.2020 10:27
Складіть зведене квадратне рівняння сума коренів якого дорівнює 7, а добуток - числу -8 Это очень...
Памагиш Памагиш  24.04.2020 10:27
Решить неравенство log 3 (x+2) + log3 х log3 (2x+1)...
galina85321 galina85321  24.04.2020 10:27
Вычисли значение y, если 8/y (разделить) = −0,8.​...
ксюха280 ксюха280  24.04.2020 10:26
1.Дана функция у= -24*х+8 в Не выполняя построения найти: 1) Значение функции, если значение аргумента равно 3 2) Значение аргумента, если значение функции равно 12 2.Построить график...
Farys Farys  18.11.2020 22:08
Найдите значение выражения (b2)-6/b-14при b=7...
annmslna2044 annmslna2044  18.11.2020 22:09
Степенная функция. С решением...
fac7 fac7  18.11.2020 22:09
Найдите значение выражения (b2)/6=b-14при b=7...

Популярные вопросы