Производная функции y=2sinx-5x в точке x=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Ребята решите. Сам работа 1 8кл 1.Продолжите предложение. А) Центральный...
3 - Черчение. Надо построить третью проекцию геометрической фигуры...
2 - Экожүйе компоненттерінің өзара байланысын түсіндіріңіз...
3 - ВСЕ ЗАДАНИЯ ПРЕКРЕПЛИНЫ ТАМ ПРО АРЕФМЕТИКУ...
2 - Дан невесомый рычаг, на одной стороне которого находятся два противовеса,...
1 - Щоб випекти 600 кг хліба потрібновзяти 4,5 ц борошна. Скількипотрібно...
2 - НАПИШИТЕ СЖАТОЕ ИЗЛОЖЕНИЕ, ОКОЛО 70-80 СЛОВ ВОТ ПЕРЕХОДИТЕ ПО...
3 - Визначити потужність сільких ГЕС, якщо на лопаті турбіни з висотою...
2 - Кому Амир Темур отдал Афганистан и Восточную Индию?по-братски...
1 - КРАТКО)А.П. Чехов. Рассказ Ионыч 1.Что увидел молодой доктор Старцев,...
3
Использованные формулы:
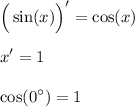
ответ: