Приветствую!, нужна по алгебре, вычислить неопределенные интегралы под "в" полностью. Заранее благодарю, и отозваться.
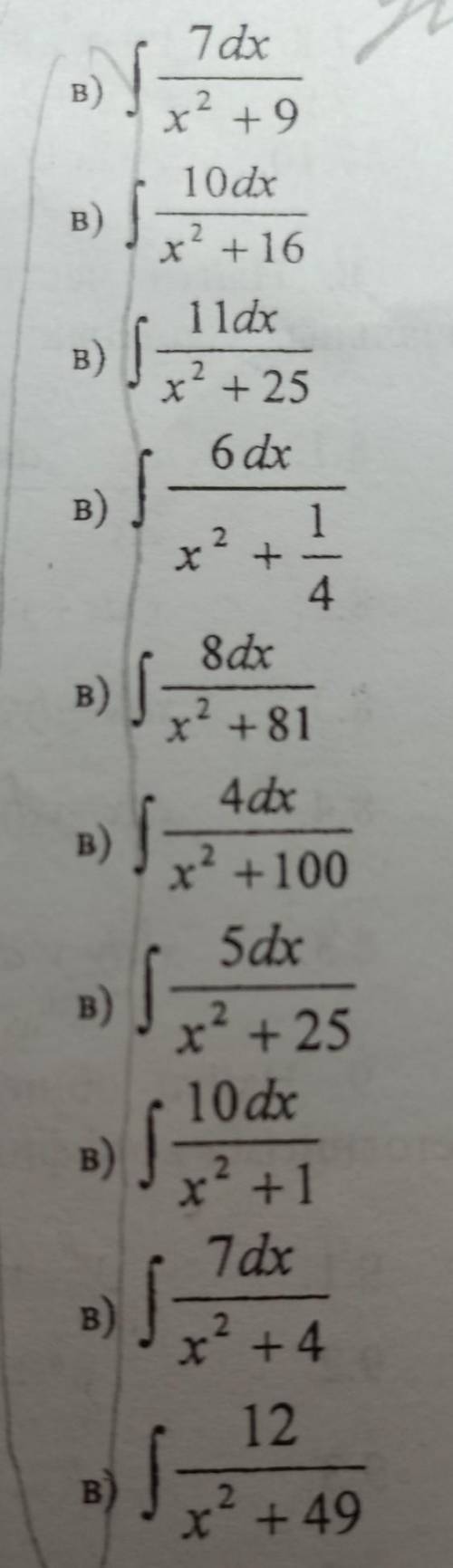
Другие вопросы по теме Алгебра
Популярные вопросы
- Боковая сторона равнобедренного треугольника равна 37 см, а высота 35 см. чему равно...
3 - Укажите номера верных утверждений. 1.-биссектриса делит угол при вершине треугольника...
2 - Вкаком случае углы amb и bmc будут смежными?...
2 - Углеводород содержит 10% водорода. относительная плотность вещества по кислороду...
1 - На кожні 100 км шляху автомобіль витрачає 8л бензини. скільки бензини потрібно,...
2 - Как правильно что человечество или кто человечество...
1 - Решить, контур площадью 6 см2 расположен в однородном магнитном поле с индукцией...
1 - 1.выберите формулы а)оснований б)кислот-из пепечня; pbo,rboh,h2o,h2co3,fecl2,fe...
2 - Нужно определить тип ! 1.(не)редко мы хотя того (не,ни) себя в других охотно . 2.хоть...
2 - Купили дыню массой 2 килограмма 400 грамм ваня отрезали одну пятую дыни а маше одну...
2
По формуле: