Пристани а и в расположены на реке,скорость течения которой на этом участке равна 3 км/ч. лодка проходит от а до в и обратно без остановок со средней скоростью 8 км/ч. найти собственную скорость лодки
Другие вопросы по теме Алгебра
Популярные вопросы
- Космический корабль стартует с земли вертикально вверх с ускорением 20 м/с в квадрате....
3 - Установите последовательность смены природных зон от экватора к полюсам...
2 - 1) почему, на ваш взгляд, столь высок процент самоубийств среди молодёжи? 2) какие...
1 - На сколько сократится длина пружины, если ее сжимать с силой 20 н? жесткость пружины...
1 - Записать слово сметана в столбик и придумать предложение записать слово корова...
1 - Довести нерівність: якщо a(4a+2b+c) 0, то b*b ac...
2 - Втрех корзинах 240 яблок. во второй корзине яблок втрое больше, чем в первой, а...
2 - Діагоналі паралелограма дорівнюють 17 см і 19 см, а його сторони відносяться як...
2 - Замените словосочетание слушали внимательно со связью примыкания, синонимичным...
2 - Всем членам семьи сейчас 77лет.состав семьи таков: муж,жена,дочь и сын.муж старше...
3
Пусть V км/ч - собственная скорость лодки, a S - расстояние между пристанями А и В.
По течению Против течения
Расстояние, км S S
Скорость, км/ч V+3 V-3
Время, ч. S/(V+3) S/(V-3)
Средняя скорость рассчитывается по формуле: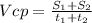
В нашем случае:
по теореме Виета:
ответ: собственная скорость лодки 9 километров в час.