1. Алгебра
  2. Пример под цифрами 5.32 !

Пример под цифрами 5.32
! Решите


Пример под цифрами 5.32 ! Решите

nicitama228800 nicitama228800    3   19.03.2022 07:37    4

Ответы
olya75357 olya75357  19.03.2022 13:00

\sqrt{3x^2-4x+1}=\sqrt{2x^2-5x+3}

Правая и левая части равенства неотрицательны, значит можно равенство возвести в квадрат .

3x^2-4x+1=2x^2-5x+3x^2+x-2=0\ \ ,\ \ x_1=-2\ ,\ x_2=1\ \ (teorema\ Vieta)

Сделаем проверку.

x=-2:\ \ \sqrt{3x^2-4x+1}=\sqrt{12+8+1}=\sqrt{21}sqrt{2x^2-5x+3}=\sqrt{8+10+3}=\sqrt{21}\ \ ,\ \ \sqrt{21}=\sqrt{21}     верно

x=1:\ \ \sqrt{3x^2-4x+1}=\sqrt{3-4+1}=0sqrt{2x^2-5x+3}=\sqrt{2-5+3}=0\ \ ,\ \ 0=0    верно

ответ:  x=-2\ ,\ x=1\ .

ПОКАЗАТЬ ОТВЕТЫ
nast60 nast60  19.03.2022 13:00

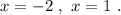
Объяснение:

5.32

\sqrt{3x^2-4x+1}=\sqrt{2x^2-5x+3} .

ОДЗ:

\left \{ {{3x^2-4x+1\geq 0} \atop {2x^2-5x+3\geq 0}} \right. \ \ \ \ \left \{ {{3x^2-3x-x+1\geq 0} \atop {2x^2-2x-3x+3\geq 0}} \right.\ \ \ \ \left \{ {{3x*(x-1)-(x-1)\geq 0} \atop {2x*(x-1)}-3*(x-1)\geq 0} \right.\ \ \ \ \left \{ {{(x-1)*(3x-1)\geq 0} \atop {(x-1)*(2x-3)\geq 0}} \right. .

(x-1)*(3x-1)\geq 0\\

(-∞)__+__[1/3]__-__[1]__+__(+∞)              ⇒

x∈(-∞;1/3]U[1;+∞)

(x-1)*(2x-3)\geq 0\\

(-∞)__+__[1]__-__[1,5]__+__(+∞)        ⇒

x∈(-∞;1]U[1,5;+∞).            ⇒

ОДЗ: x∈(-∞;1/3]U[1]U[1,5;+∞)

(\sqrt{3x^2-4x+1})^2=(\sqrt{2x^2-5x+3} )^2\\3x^2-4x+1=2x^2-5x+3\\x^2+x-2=0\\D=9\ \ \ \ \sqrt{D}=3\\ x_1=-2\in\ \ \ \ x_2=1\in.

ответ: x₁=-2,  x₂=1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sanek2031 sanek2031  21.08.2019 10:00
При каком значение x уравнение 10х-5=0?...
nikgtacs59 nikgtacs59  21.08.2019 10:00
Докажите тождество: 1-2sinacosa/sina-cosa=sina-cosa...
Nika0345 Nika0345  21.08.2019 10:00
Налог на доходы составляет 13% от заработной платы. заработная плата и. к равна 12500 руб. сколько руб. он получит после вычета налога на доходы ?...
MashaSay MashaSay  21.08.2019 10:00
Log2(x+5)=log3(x+5) решите подробно...
oksanasmolko20 oksanasmolko20  21.08.2019 10:00
1) точка движется по закону x(t)=t^3+1 найдите скорость точки в момент 3 сек. 2) найдите угол наклона касательной к графику функции f(x)=(x^2-3x/4) в точке x0=1....
chalenkotaya chalenkotaya  21.08.2019 10:00
При каком значении р уравнения х^2-2х+1=р имеет 1 корень?...
Kros228volk225 Kros228volk225  21.08.2019 10:00
Найдите корень уравнения (2х-3)*(5х+1)=2х+2/5...
SureckMozg SureckMozg  21.08.2019 10:00
Найдите сумму 5 первых членов прогрессии если b1 =5 ; b3 =80...
N4kes N4kes  21.08.2019 10:00
Преобразуйте в многочлен.a) (a-3)² б) (2x+y)² в)(5b-4x)(5b+4x)...
Kinder2571 Kinder2571  21.08.2019 10:00
2* cos5x * sin7x - sin12x, если sinx-cosx=0,4...

Популярные вопросы