Пример непостоянной функции f(x), определенной для всех действительных x и имеющей свойства
Ответы
Поделим множество всех действительных чисел на два подмножества. Первое состоит из чисел вида 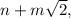 где n и m - целые. Второе состоит из всех остальных. Ясно, что оба подмножества непусты, так как первое счетно, а множество действительных чисел несчетно, а если из несчетного множества убрать счетное подмножество, то останется множество той же мощности. Пусть функция во всех точках первого множества принимает какое-то одно значение, скажем 1, а во всех точках второго множества - другое значение, скажем 0. Добавление к числам первого множества любого количества единиц и любого количества корней из 2 не выводит из него. То же справедливо для чисел второго множества, так как если в результате добавления к x числа вида
где n и m - целые. Второе состоит из всех остальных. Ясно, что оба подмножества непусты, так как первое счетно, а множество действительных чисел несчетно, а если из несчетного множества убрать счетное подмножество, то останется множество той же мощности. Пусть функция во всех точках первого множества принимает какое-то одно значение, скажем 1, а во всех точках второго множества - другое значение, скажем 0. Добавление к числам первого множества любого количества единиц и любого количества корней из 2 не выводит из него. То же справедливо для чисел второго множества, так как если в результате добавления к x числа вида 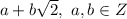 получится число вида
получится число вида 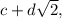 , то x равен разности этих чисел, то есть само есть комбинация 1 и корня из 2 с целыми коэффициентами. Поэтому построенная функция удовлетворяет требуемому условию.
, то x равен разности этих чисел, то есть само есть комбинация 1 и корня из 2 с целыми коэффициентами. Поэтому построенная функция удовлетворяет требуемому условию.
ПОКАЗАТЬ ОТВЕТЫ
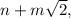 где n и m - целые. Второе состоит из всех остальных. Ясно, что оба подмножества непусты, так как первое счетно, а множество действительных чисел несчетно, а если из несчетного множества убрать счетное подмножество, то останется множество той же мощности. Пусть функция во всех точках первого множества принимает какое-то одно значение, скажем 1, а во всех точках второго множества - другое значение, скажем 0. Добавление к числам первого множества любого количества единиц и любого количества корней из 2 не выводит из него. То же справедливо для чисел второго множества, так как если в результате добавления к x числа вида
где n и m - целые. Второе состоит из всех остальных. Ясно, что оба подмножества непусты, так как первое счетно, а множество действительных чисел несчетно, а если из несчетного множества убрать счетное подмножество, то останется множество той же мощности. Пусть функция во всех точках первого множества принимает какое-то одно значение, скажем 1, а во всех точках второго множества - другое значение, скажем 0. Добавление к числам первого множества любого количества единиц и любого количества корней из 2 не выводит из него. То же справедливо для чисел второго множества, так как если в результате добавления к x числа вида 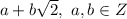 получится число вида
получится число вида 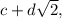 , то x равен разности этих чисел, то есть само есть комбинация 1 и корня из 2 с целыми коэффициентами. Поэтому построенная функция удовлетворяет требуемому условию.
, то x равен разности этих чисел, то есть само есть комбинация 1 и корня из 2 с целыми коэффициентами. Поэтому построенная функция удовлетворяет требуемому условию.
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите со всеми пояснениями как можно быстрее...
1 - За хімічною формулою обчислити масові частки елементів в речовині...
2 - M a) 7.56headings. Use them to write or say a fewsentences about...
2 - 2. Восстановите последовательность событий: а) июньское восстание...
3 - 06:061 +095 612 - 0S006)(302 281 - 12 6491:48 +3966(21000 - 308...
3 - подумай сравню показания 2 электроскопов какой из них показывает...
3 - Варіант 3 1. Основи AD і BC трапеції ABCD дорівнюють 9 см і 4...
3 - 10-тапсырма. Жануарлар туралы берілген қызықты мәліметтерді пай...
1 - написать сообщение о том что такое простой и сложный состав строения...
3 - Сообщение на тему ,, Экологические проблемы углеродной энергетики...
3