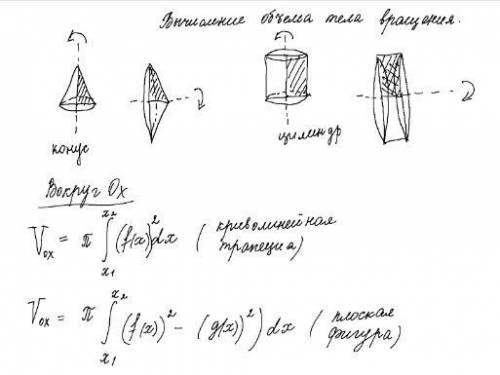
Применение вычисления интегралов. Вычислите объем тела вращения.
y=4x-x^2
y=0
Другие вопросы по теме Алгебра
Популярные вопросы
- До яких наслідків призводить осушування боліт?...
3 - Выберите из перечисленного спутник Сатурна:ИоТитанКалипсоЕвропа...
3 - В Хогвартсе олимпиада по астрономии. На диаграмме Аврора Синистра, преподаватель,...
1 - (5y-7)×(y-0,4) =0 Чему равен перый, а чему второй игрик?...
3 - Биыктыгы 7м уйдын тобесынен массасы 500г сунгы муз узылып тусты муз кулаганда...
1 - Расстояние между сёлами 45 км. Через сколько часов встретятся два пешехода,которые...
1 - Изображение автора саней, волочащихся пешком...
1 - Привет, можете рассказать смешную историю. (для школьного сочинения надо)...
1 - Вкажіть правителя, за якого Афіни досягли найбільшого політичного та культурного...
2 - Помгите легко и не трудно ...
3
Объяснение:
ответ: V≈107.233 куб. ед.
V=\pi \int\limits^4_0 {(4x-x^2)}^2 \, dx=\pi \int\limits^4_0 {(16x^2-8x^3+x^4)} \, dx
=16/3 x^3 -8/4 x^4 +1/5 x^5 |^4_0= 16/3*64-2*256+ 1/5*1024=34,1333*\pi
Объяснение:
4x-x^2=0
x=0 x=4