1. Алгебра
  2. прикрепленный файл,1 задача

прикрепленный файл,1 задача 7 класс


прикрепленный файл,1 задача 7 класс

sek071001p0ancj sek071001p0ancj    1   24.11.2020 07:22    1

Ответы
Gamaun Gamaun  24.12.2020 07:25

(\frac{16}{3},\ \frac{13}{9} )

Объяснение:

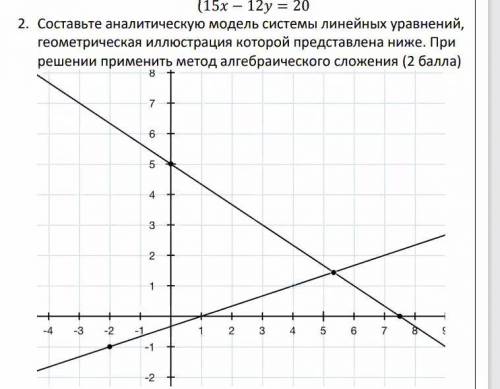
На графике представлены функции вида:

y = kx+b

Вычислим уравнения прямых:

1) (0;\ 5), (7,5;\ 0)\\\left \{ {{5 = k*0+b} \atop {0 = k*7,5+b}} \right. \\\left \{ {{b=5} \atop {7,5k+5 = 0}} \right.\\\left \{ {{b=5} \atop {k = -\frac{2}{3} }} \right. \\\\y = -\frac{2}{3} x + 5

2) (-2;\ -1),\ (1, 0)\\\left \{ {{-1 = k*(-2) + b} \atop {0 = k*1 + b}} \right.\\\left \{ {{b = -k} \atop {-1= -2k+(-k)}} \right.\\\left \{ {{k = \frac{1}{3} } \atop {b = -\frac{1}{3} }} \right. \\\\y = \frac{1}{3}x-\frac{1}{3}

Тогда аналитическая модель системы линейных уравнений выглядит следующим образом:

\left \{ {{y=-\frac{2}{3}x+5 } \atop {y = \frac{1}{3}x - \frac{1}{3} }} \right.

Вычитаем второе из первого и получаем:

y-y = -\frac{2}{3}x -\frac{1}{3}x + 5 -(- \frac{1}{3}) \\0 = -x +5\frac{1}{3}\\x = 5\frac{1}{3} = \frac{16}{3}

Подставляем найденный x в любое из уравнений и находим y:

y = \frac{1}{3} * \frac{16}{3} - \frac{1}{3} = \frac{16}{9} - \frac{3}{9} = \frac{13}{9}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nastyyanokogloStasya nastyyanokogloStasya  20.09.2020 07:17
Исследуйте на монотонность функции: а)y=8x+3 в)y=x/3+1 б)y=5-2x г)y=1/3-2x/5...
dongrigoriew20 dongrigoriew20  20.09.2020 06:17
Треугольник делится медианой,проведенной к основанию на 2 треугольника, периметр которых 18 см и 24 см. Найдите большую боковую сторону,если меньшая боковая сторона равна 6...
sotskova20041 sotskova20041  20.09.2020 06:17
1.104. Сандарды негізі 2 болатын дәрежемен алмастырыңдар:...
zakergaevak zakergaevak  20.09.2020 01:05
Решить 3.15 (1) и 3.16 (1)....
hoylli333 hoylli333  09.03.2021 21:55
Сколько целых чисел расположена между тремя корнями из 15 и пятью корнями из шести...
апро27 апро27  09.03.2021 21:56
Условие задания: 1 Б. Дракон, который сидел в пещере и охранял сокровища, украденные угномов, через некоторое время согласился выплачивать процент жителям Дейла, которые подрядились...
Данана1 Данана1  09.03.2021 21:56
Запиши в виде многочлена квадрат двучлена, заполнив пропуски​...
емдетей емдетей  09.03.2021 21:59
Вычислите интеграллы}(3 {x}^{2} + 2x - 1)dx​...
jenkatimosh jenkatimosh  09.03.2021 22:01
Вход отдельно скобки и числа вместе со знаками; если +∞, то пишите в поле +B, если −∞, то пиши −B! i+i+i+i+i −2 i∈ =...
cazydays cazydays  09.03.2021 22:01
Чому дорівнює х, якщо (1/9)^х = 27...

Популярные вопросы