1. Алгебра
  2. Прибор содержит две микросхемы.

Прибор содержит две микросхемы. Вероятность выхода из строя в течение 10 лет первой микросхемы равна 0,07, а второй – 0,10. Известно, что из строя вышла одна микросхема. Какова вероятность того, что вышла из строя первая микросхема?

glebtomilovpop0 glebtomilovpop0    1   09.03.2020 03:57    32

Ответы
erdgfgh erdgfgh  11.10.2020 21:05

Обозначим событие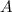 A - вышла из строя одна микросхема и введём гипотезы 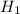H_1 - отказала первая микросхема, 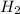H_2 - отказала вторая микросхема.

P(H_1)=0{,}07\cdot (1-0{,}1)=0{,}063\\ P(H_2)=(1-0{,}07)\cdot 0{,}1=0{,}093

Условные вероятности: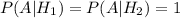 P(A|H_1)=P(A|H_2)=1.

По формуле полной вероятности, вероятность события А:

P(A)=P(A|H_1)P(H_1)+P(A|H_2)P(H_2)=0{,}063+0{,}093=0{,}156

По формуле Байеса, вероятность того, что вышла из строя первая микросхема, равна

P(H_1|A)=\dfrac{P(A|H_1)P(H_1)}{P(A)}=\dfrac{1\cdot 0{,}063}{0{,}156}=\dfrac{21}{52}\approx 0{,}404

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
gjkbyf1984 gjkbyf1984  02.10.2019 19:10
много принадлежат ли точки а(-0,05; -200),b(-0,1; 100),c(400; 0,25),d(500; -0,02) графику функции y=10/x?...
R456 R456  02.10.2019 19:10
Найдите значение выражения ✓0,81 x 25...
подкайфом подкайфом  02.10.2019 19:10
Решите уравнение x²=54 (решение подробно)...
chernenkopolina chernenkopolina  02.10.2019 19:10
Возвести в степень х в квадрате равно 4...
26032004й 26032004й  03.06.2020 13:00
с математикой база с математикой база >...
bdhdt bdhdt  03.06.2020 13:03
Найти x^17 + 1/x^17, если x^2 + x + 1 = 0(при некоторых недействительных x)...
Ника12040000 Ника12040000  04.06.2020 01:04
РЕШИТЬ НАДО ДО ЗАВТРА С ПОДРОБНЫМ РЕШЕНИЕМ...
Lulu117 Lulu117  04.06.2020 01:26
Метод подстановки. Неопределенный интеграл....
Hika34 Hika34  03.06.2020 13:27
Решите уравнение sin^2(x)+6sin(x)-6=0...
arscool arscool  03.06.2020 13:27
с алгеброй!провести полное исследование и построить график функцииy=ln x...

Популярные вопросы