При якому значенні b має один корінь рівняння
(b+1)x²+x(b+3)+2=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить массу соляной, необходимой для получения 22.2 г хлорида...
1 - Сочинение на тему моя любимая вещь, в стили речи описании...
2 - Переведите текст на язык: for sale. weter tower for sale. the...
1 - Ішін ені 5 см ұзындығы 1 дм 2 см қорапшалармен толтыру үшін табаны...
3 - Көп нүктенің орнына есімшелердің жұрнақтарын қойып жазыңдар....
1 - Спряжение время лицо число и род слова устанешь...
2 - Вчем чувства человека отличаются от его эмоций...
2 - Какое количество теплоты потребуется чтобы расплавить 200 г свинца...
3 - Что удерживает нас от проявления звериных привычек?...
1 - Соединение между костями черепа в скелете - это...
3
Если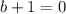 откуда
откуда 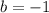 , то квадратное уравнение примет линейный вид
, то квадратное уравнение примет линейный вид 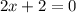 отсюда имеет единственный корень x = -1.
отсюда имеет единственный корень x = -1.
Теперь если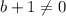 , то квадратное уравнение имеет единственный корень, если его дискриминант равен нулю
, то квадратное уравнение имеет единственный корень, если его дискриминант равен нулю
D = 0; (b-1)² = 0 откуда b = 1
ответ: при b = ± 1.