При якому найбільшому значенні параметра а рівняння | + 8| х |+12|=а матиме 4 корені ?
перевод
При котором наибольшем значении параметра а уравнение | + 8| х |+12|=а будет иметь 4 корни?
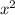
Другие вопросы по теме Алгебра
Популярные вопросы
- Математика 6класс460есеп. ...
3 - 510. Амалдарды орындаңдар: 1) (7/15-1/6)+2/5; 2) (3/8-1/9)+25/36; 3) (8/9-5/6)+2/3;...
1 - Вершинами трикутника є точки D(1;5) M(-4;7)N(8;-3) знайдіть довжину медіани...
1 - ответьте на вопросы: 1. Почему категорически запрещается пробовать вещества...
3 - ПОЭАЛУЙСТА Ниф-ниф, Наф-наф и Нуф-Нуф решили построить один крепкий дом на...
3 - Как оксид водорода влияет на жизнь водомерки? Это соч заранее Кто знает Биологию...
1 - 4. Замени квадрат числа лей и вычисли.а) (4²+8²)-10(10²+9²)+220б) 6²+(8²+136)3²+(6²-4²)Памагите...
2 - Знайти продуктивність автомобіля за рік, якщо його вантажопідйомність складає...
1 - Прочитайте текст «Начало и продолжение космической эры» (упр.129, с.72). Составьте...
1 - Какие два из перечисленных понятий используются в первую очередь при описании...
1
Вероятно, такого значения параметра а не су-
ществует. Если уравнение разделить на левую и правую части, то графиком левой части яв -
ляется квадратичная парабола, ветви кото -
рой направлены вверх, а вершина находится в точке (0; 12).
У = |х^2+8×|х|+12|
Правая часть уравнения : У=а
Левая и правая части при пересечении могут
дать максимум две точки.
Мой вариант ответа : при а>12 уравнение
может иметь два корня.
Объяснение:
.
При котором наибольшем значении параметра а уравнение | x² + 8|х | +12 | = а будет иметь 4 корни ?
ответ: a ∈ ∅
Объяснение: | x² + 8|х| +12 |= а ⇔ | |x|² + 8|х| +12 | = а
замена : t = |x | ≥ 0
| t² + 8t +12 | = а
Ясно,что это уравнение может иметь решение , если а ≥ 0
Фиксируем : а ≥ 0
Если a =0 : t² + 8t +12 = 0
( D = 4 > 0 два корня и они оба отрицательны )
{t₁ + t₂ = - 8 < 0 ; t₁ * t₂ = 12 > 0
* * * t₁ = - 6 ; t₂ = - 2. * * * ⇒ x ∈ ∅
[ t² + 8t+ 12 = - a ; (совокупность
[ t² + 8t + 12 = а . уравнений )
1 . t² + 8t+ 12 = - a
t² + 8t+ 12 + a =0 , D/4 = 4² - (12+a) = 4 - a
D< 0 ⇔ 4 - a < 0 ⇔ a > 4 → нет корней ( действительных )
D= 0 ⇔ 4 - a = 0⇔ a = 4 двукратный корень t₁ = t₂ = - 4 < 0 → исходное уравнение не имеет корней
D > 0 ⇔ 4 - a > 0⇔ а < 4 → два отрицательных корней
t₁ = -4 - √(4 - a) < 0 ; t₂ = - 4 + √(4 - a) < 0
опять → исходное уравнение не имеет действительных корней
- - - - - - - - - - - - - - - -
2. t² + 8t + 12 = а .
t² + 8t + 12 - а = 0 D/4 = 4² - (12- a) = 4+ a
D< 0 ⇔ 4 + a < 0 ⇔ a < - 4 невозможно ( т.е. для всех a > 0 всегда имеет корней )
D = 0 ⇔ 4 + a = 0⇔ a = - 4 двукратный корень t₁ =t₂ = - 4 < 0 → исходное уравнение не имеет действительных корней
D > 0 ⇔ 4 + a > 0 ⇔ a > - 4 → два корня , притом из них один
t₁ = - 4 - √(4 + a) < 0 отрицательный
t₁ = - 4 - √(4 + a) < 0 ; t₂ = - 4 + √ (4 + a)
Второй корень может принимать значение разных знаков и нуль
t₂ < 0 ⇔ - 4 + √ (4 + a) <0 ⇔√ (4 + a) < 4 ⇔ 0 < a< 12
→ исходное уравнение не имеет корней ( x ∈ ∅ )
t₂ = 0 ⇔ - 4 + √ (4 + a) =0 ⇔√ (4 + a) = 4 ⇔ 4 + a = 16 ⇔ a= 12
→ исходное уравнение имеет один корень x = 0
t₂ > 0 ⇔√(4 + a) > 4 ⇔ 4 + a > 16 ⇔ a > 12
* * * а > 12 исходное уравнение имеет 2 корня * * *
резюме
нет корней : x ∈ ∅ , если - ∞ < a < 12 ;
один корень : x = 0 , если a= 12 ;
максимум два корня , если a > 12 .