1. Алгебра
  2. При яких значеннях параметра

При яких значеннях параметра а рівняння

має два розв'язки​

Tanya20042017 Tanya20042017    2   11.04.2020 13:06    0

Ответы
Galya03 Galya03  13.10.2020 02:18

\dfrac{x^2-8x+7}{x-a}=0\; \; \; \Rightarrow \; \; \; \left\{\begin{array}{l}x^2-8x+7=0\\x-a\ne 0\end{array}\right\; \; \; \left\{\begin{array}{l}x_1=1\; ,\; x_2=7\; (teor.\; Vieta)\\x\ne a\end{array}\right\\\\\\\Rightarrow \; \; \left\{\begin{array}{l}x_1=1\; ,\; x_2=7\\a\ne 1\; ,\; a\ne 7\end{array}\right

Уравнение имеет два решения при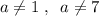  a\ne 1\; ,\; \; a\ne 7  ,  то есть при

a\in (-\infty ,1)\cup (1,7)\cup (7,+\infty )\; .

ПОКАЗАТЬ ОТВЕТЫ
Chcdhj Chcdhj  13.10.2020 02:18

\frac{ {x}^{2} - 8x + 7 }{x - a} = 0

ОДЗ:

x≠a

Розкладемо числівник на множники за теоремою Вієта:

\frac{(x - 1)(x - 7)}{x - a} = 0

Отримали 2 корені:

x_{1} = 1 \\ x_{2} = 7

Тобто рівняння завжди має 2 корені без урахування ОДЗ. Але можливі ситуації, коли параметр а може буде рівний одному з коренів і тоді рівняння матиме лише один корінь тому параметр а не може буди рівним кореням:

a≠1 \\ a≠7

Відповідь:

a \in( - \infty ;1) \cup(1;7) \cup(7; + \infty )

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ymnый0 ymnый0  21.01.2021 08:46
Корень из x(x-0 2)(x+6) при каких значениях x вырадение имеет смысл...
pennycat pennycat  21.01.2021 08:44
Заданы координаты вершин треугольника A(-4;2), B(5;5), C(3;-3). Найти: 1) уравнения сторон АВ и АС; 2) тангенс угла А; 3) уравнение высоты, опущенной, из вершины В....
arturveryelecki arturveryelecki  21.01.2021 08:43
Выбери верные утверждения для функции y = 3x2 – 5. Верных ответов: 3 Множество значений функции (–5; +∞) График функции проходит через точку (2; 7) Промежуток убывания x ∈ (–5;+∞);...
ser2003123 ser2003123  21.01.2021 08:42
Сумма и разность кубов двух выражений 8m³+n⁶=(​...
fumymovie fumymovie  09.09.2019 19:00
Объясните тему корни (все действия). посоветуйте какие-нибудь сайты. каждый ответ будет важен....
Windows95 Windows95  09.09.2019 19:00
Имеются два куска меди 42% и 65% соответственно. в каком отношении нужно взять эти сплавы, чтобы, переплавив, получить сплав, содержащий 50% меди?...
shidiemmacom1 shidiemmacom1  09.09.2019 19:00
Решить систему уравнений 2х+y-7=0 x-y-2=0 это в системе...
ирина1834 ирина1834  09.09.2019 19:10
При каких значениях имеет смысл выражение √-3y^3?...
ахпхпха ахпхпха  12.03.2021 07:39
Два туриста из одной деревни в другую с расстоянием 20 км одновременно вышел. Скорость первого туриста на 1 км/ч больше, чем второго из-за избытка он пришел на 1 час раньше второго....
1232508 1232508  12.03.2021 07:38
Установите соответствие списка и его html-кода: 11 ul type=circle li first /ul ul type=square li second /ul 2 ul type=circle li first li secondary /ul 3 ul type=disk li first ul...

Популярные вопросы