При яких значеннях а рівняння х²+(а+5)х+1=0 має дійсні корені?

Відповідь:

f(x) має дійсни корені при а ∈ (-∞;-7]∪[-3;+∞]

Пояснення:

Рівняння має дійсні корені, коли дискримінант рівняння ≥0.

тому запишемо

D=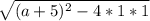

тому (а+5)²-4*1≥0;

а²+10а+25-4≥0

а²+10а+21≥0.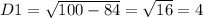      a1=-10-4/2=-7  a2=-10+4/2=-3

Графіком рівняння а²+10а+21=0  є парабола з точками перетину з віссю ОХ

(-7;0) та (-3;0) вітки параболи направлені догори тому вона буде додатня на відрізках а ∈ (-∞;-7]∪[-3;+∞]

Відповідь: f(x) має дійсни корені при а ∈ (-∞;-7]∪[-3;+∞]