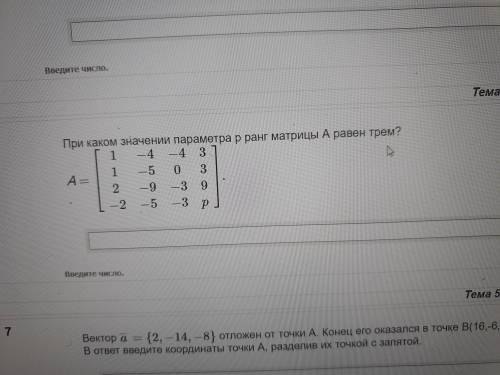
При каком значении параметра р ранг матрицы А равен трем?
Другие вопросы по теме Алгебра
Популярные вопросы
- Три человека возили в тележках камни. у одного из них спросили: — что ты здесь...
2 - Как называется словарь абрамова в 1900 году ? где выпустил абрамов словарь ?...
2 - Как проверить первую букву и в слове блестящими...
1 - Решение (3x-1)^2=3(1-2x) (x+3)^2=3(x+1)^2...
1 - Складне речення зи словом море, писня, щиристь на выбир...
1 - Это легко! я просто проверю вас, какие бывают позезные ископаемые?...
3 - Тұмар патшайым сақтың ұлы патшайымы мəтін...
2 - Решить .для оформления детской книги художнику нужно сделать 55 рисунков.в первую...
2 - Сумма восьми различных натуральных чисел равна 53 . наименьшое число 3. назовите...
3 - Вкниге 85 страниц.в течении недели костя читал по 10 страниц в день.сколько страниц...
3
Оувмлущвсгвлцдудагг
1. Найдем расширенную матрицу. Добавим столбец свободных членов {1, 2, р} к исходной матрице А.
| 2 0 1 | 1 |
А = | 4 -1 3 | 2 |
| -2 р 5 | р |
2. Теперь найдем определитель расширенной матрицы. Для этого воспользуемся правилами для вычисления определителя 3x3 матрицы.
Определитель расширенной матрицы = (2 * (-1) * 5) + (1 * 3 * (-2)) + (0 * 4 * р) - (1 * (-1) * (-2)) - (2 * 3 * 2) - (р * 4 * 5)
= (-10) + (-6) + (0) - (2) - (12) - (20р)
= -28 - 20р
3. Зная, что ранг матрицы равен трем, это означает, что определитель расширенной матрицы должен быть равен нулю.
То есть, -28 - 20р = 0
4. Теперь найдем значение параметра р, решив уравнение:
-28 - 20р = 0
Добавим 28 к обоим сторонам:
-20р = 28
Делим на -20:
р = 28 / -20
р = -7/5
Таким образом, при значении параметра р равного -7/5 ранг матрицы А будет равен трем.