При каком значении параметра a уравнение не имеет корней?

Дробь равна нулю, когда ее числитель равен нулю, а знаменатель не равен нулю. Это высказывание можно записать в виде системы следующим образом:

Решим первое уравнение системы:

Решим второе уравнение-ограничение системы: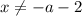

Таким образом, уравнение не будет иметь корней, если его корень совпадет с ограничением на данное уравнение:

Следовательно, при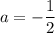 уравнение не будет иметь корней.

Проверка. Действительно,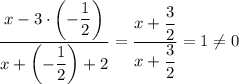

ответ: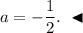

ответ: -1/2

Объяснение:

это система :  x-3a=0  и  x+a+2 не=0,  

x=3a  и   х  не=-a-2,  подставим 1-е  во  2-е,

3a не =-a-2,   4a не= -2,  a не= -1/2 .