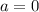При каком значении параметра а, имеет бесконечное количество решений
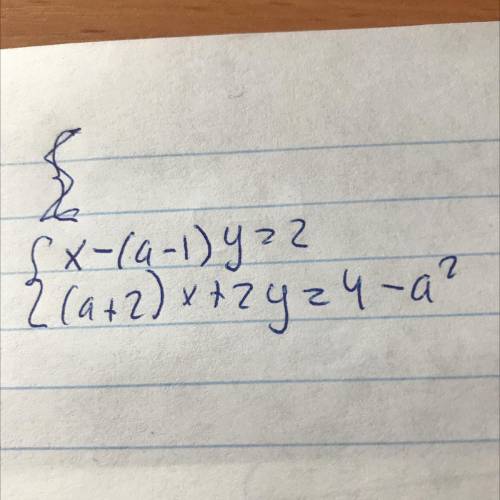
Другие вопросы по теме Алгебра
Популярные вопросы
- Всегда ли нужно выбирать между свободой и любовью?...
2 - Задача №2 Определить товарные запасы в днях на 1.04 - годовой объем продажи...
3 - Почему мне понравился главный герой романа над пропастью во ржи...
2 - Дайте ответы на 29,30,31 урок в РЭШ, 9 кл англ яз Контрольные задания...
3 - Какая страна находиться на севере Греции?...
1 - ответить на во по английски к тексту....
2 - Рассмотрите шутливые рисунок Предположите Какие Советы дает тренер игрокам...
3 - Рубашка стоила 900 р. Сначала её цену понизили на 15%, а потом новую цену...
3 - Колебательный контур состоит из катушки индуктивностью L и конденсатора...
3 - решить самостоятельную по химии...
1
Система эквивалентных уравнений имеет бесконечное количество решений, это означает, что отношения коэффициентов при неизвестных и свободных членов должны быть равны.
Получаем равенство.
Решаем попарно.
1) Равенство первой и второй дробей
2) Равенство первой и третьей дробей
3) Равенство второй и третьей.
Общее решение:
ответ: при