При каком значении a уравнение 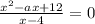имеет единственный корень? В ответе запишите произведение всех найденных значений a

Дробь равна 0, когда числитель равен 0, а знаменатель отличен от нуля:

     ⇒      

Подставим х=4  в  квадратное уравнение

получаем

При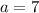    квадратное  уравнение имеет два корня,

один из которых равен 4, значит требование задачи будет выполнено,

и уравнение будет иметь один корень.

Кроме того квадратное уравнение

будет иметь один корень, если дискриминант этого уравнение равен 0

   ⇒           ⇒       ⇒

    или  

О т в е т.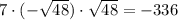

а=-7;

Объяснение:

ОДЗ: х≠4

х²-ах+12=0

(х-4)(х-3)=0=> х≠4; х=3;

х²-7х+12=0