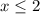При каких значениях x выполняется равенство: 1) |x+3|=x+3 2) |x-2|=2-x напишите как именно решать! а не просто ответ.
Другие вопросы по теме Алгебра
Популярные вопросы
- The moon isn’t … the sun. Варианты: less brighter as bright as much bright...
1 - Переделать текст , но сюжет оставить примерно таким же.МНОГО БАЛОВ что бы...
2 - Равносильны ли уравнения |x-2|= -3 и 3^x = (-1)^3...
2 - Повторить неправильные глаголы повторить грамматику сделать задание ❤️❤️...
1 - Напиши предложение с Келер шақ (мақсаты,болжалды,ауыспалы) слова с которыми...
2 - 1)члены семьи самсона вырина 2)черты характера героя, в каких поступках...
2 - Два груза массами 400г и 700г связаны нитью, переброшенной через неподвижный...
2 - , сделать только пункт ( б )...
2 - Какой характер Пульхерии Ивановны из повести Старосветские помещики...
3 - Семиклассник Иван пришел из школы домой и решил скачать с сети Интернет...
2
Воспользуемся правилом работы с модулем:
Здесь a — какое-то выражение.
1) Если заменить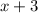 на
на  , то получится
, то получится 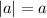 . Значит, по правилу работы с модулем
. Значит, по правилу работы с модулем 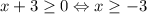
2) Если заменить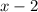 на
на  , то получится
, то получится 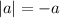 . Значит, по правилу работы с модулем
. Значит, по правилу работы с модулем 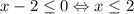 (2 тоже включаем, несмотря на строгое неравенство в правиле, потому что при x=2 x-2=0, а |0|=0 тоже верно).
(2 тоже включаем, несмотря на строгое неравенство в правиле, потому что при x=2 x-2=0, а |0|=0 тоже верно).
ответ: 1)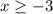 2)
2)