При каких значениях С уравнение не имеет корней?
х4–12х2 + С = 0
ulia09200413
1
13.12.2020 13:18
0
Другие вопросы по теме Алгебра
MartynaEvgeneva
27.05.2019 18:30
dfefert4tNNN
27.05.2019 18:30
Mramericka1988
27.05.2019 18:30
anya12345678900
27.05.2019 18:30
vladkabanets
06.08.2019 09:10
linasysueva01
06.08.2019 09:10
рдабаббмдедпббб
06.08.2019 09:10
gggggerrrr
06.08.2019 09:10
star5647
06.08.2019 09:10
Популярные вопросы
- Напишите мне какие однородные члены здесь есть.и скажи где они...
1 - Надо написать характеристику этого предложения(например: восклицательное,простое,сложное,вопросительное...
3 - Всем я тут 1 раз ! с ! наша училка орет нужно в решении дано...
3 - 1.используйте в предложениях слова из словарного минимума.1london...
3 - Не большое. сочинение на тему как телевизор влияет на жизнь .нужно...
1 - Какие типичные социальные роли определяют социальную сущность...
3 - Умоляю почему наличие воды - одно из главных условий прорастания...
1 - Решить функцию 4(х-2)-3(у+3)=1 3(х+2)-2(х-у)=5...
1 - Решите уровнения (x+27)-12=42 115-(35+y)=39 зарание зарание...
3 - Спиши предложения вставляя пропущенные буквы и знаки препинания....
2
Введём замену: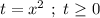
. В результате получаем простое квадратное уравнение:
Квадратное уравнение не имеет решений, когда его дискриминант меньше нуля. Дискриминант данного уравнения равен:
Получаем неравенство:
ответ: данное уравнение не будет иметь корней при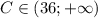
.