При каких значениях параметра уравнения 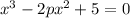 и
и 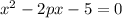 имеют общий корень?
имеют общий корень?
Другие вопросы по теме Алгебра
Популярные вопросы
- Укошки 6 котят больше половины рыжие , а остальные белые...
1 - 2/3+1/4 , 4/5-3/4 , 1/2+2/5 , 1/2-2/5 , 3/4+2/3 , 3/5-1/3 , 3/5+1/3...
3 - Дополните чертеж обозначениями концов отрезков, если ab= 1дм 4см 5мм...
3 - Разложите число 234 напростые множетели...
2 - Использовать закономернность 803*52=?...
2 - Запиши строкислов в которыхданы однокореные слова лес леса в лесу...
2 - Подобрать синонимы к данным словам.аромат,скупой,бежать,грустный,чудесный,дитя,зной,десять,нападение....
2 - Артём тратил на дорогу до школы 15 минут а до булочной 8 минут на...
3 - Из данных чисел составьте пары взаимно простых чисел: 315,154,135...
2 - Акционрное общество имеет 1215гиктара засееной земли.пщеница занимает30%всей...
1
выражу р из обоих уравнений и приравняю их, этим я найду координату х точки пересечения графиков на оси х. Потом подставив ее в любое из уравнений найду р
из первого
2px^2=x^3+5; p=(x^3+5)/(2x^2)
из второго
2px=x^2-5
p=(x^2-5)/(2x)
x≠0!
(x^3+5)/(2x^2)=(x^2-5)/(2x)
2x^2(x^2-5)=2x(x^3+5)
x(x^2-5)=x^3+5
x^3-5x=x^3+5
x=-1
подставлю в первое
-1-2p+5=0
p=2