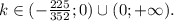При каких значениях параметра k уравнение ky2 – 3(4k + 5)y + 36k + 2 = 0 имеет два различных корня?
!ПОСЛЕДНИЕ !
Другие вопросы по теме Алгебра
Популярные вопросы
- Надо заменить звездочку подходящим одночленом и представить в виде...
3 - Решите ( подробно), . заранее )(ответ: а) 129,5 км б) 70% в) на 42,...
3 - Ханских советник 4 буквы сборщик налогов 6 букв...
2 - Правило : pr.s-i go to school everyday *отрицание и вопрос. правило:...
2 - Виконайте зазначені дії і зведіть многочлени до стандартного вигляду:...
1 - План рассказа приёмыш и выписать всё про приёмыша(лебедя)...
3 - 7и 12. можно просто формулы и пояснения...
1 - Решить 1)open the brackets to complete the sentences 1. the tea her...
1 - Сторона правильного восьмиугольника abcdefgh имеет длину 2. чему равна...
3 - Лыжник должен проехать 48 км. сколько времени он потратит на этот путь...
1
Квадратное уравнение имеет два различных корня, если его дискриминант положительный
Если коэффициент перед y² равен нулю, то квадратное уравнение превратится в линейное, что будет иметь единственное решение. То есть, при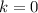 имеется единственный корень
имеется единственный корень 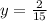
ответ: