При каких значениях параметра a уравнение x^2-2ax+8=0 не имеет решения?

x²-2ax+8=0

D=4a²-32

4a²-32<0

a²<8

a<√8

a<2√2    a∈(-∞;2√2)

Уравнение не имеет корней если дискриминант меньше нуля.

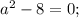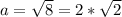Если , то и

Решаем или методом интервалов или чертим схему параболы, ветви которой направлены вверх. Получим, что значения функции меньше нуля при х∈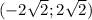

если начертить прямую и отметить данные точки , то знаки будут +, -, +