При каких значениях параметра a уравнение 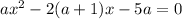 имеет, по крайней мере, одно положительное решение
имеет, по крайней мере, одно положительное решение
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишіть текст фонетичною транскрипцією.! група українських говірок являє окремий,...
2 - Виділіть з поданого тричлена квадрат двочлена: а)x²-6x+15 б) х²+8х+8 в) x²+5x+6...
1 - Даны точки а(2; -1) в(2; 4) с(6; -1) 1.найдите координаты векторов ав,св 2.найдите...
2 - Выполни синтаксический разбор. она наполнилась чистейшей прозрачной водой.в ней...
3 - Определите количество натуральных чисел от 10 до 20 включительно, для которых истинно...
2 - Алкадиены, нахождение в природе. , заранее )...
1 - Напиши короткий рассказ по одной из следующих тем: основа межличностных отношений....
1 - Как отразилась война на судьбе и творчестве...
1 - Почему перед машу миронову стоит запятая? в этом произведении рассказывается про...
1 - The browns in large house when their children were at home, but they moved to small...
1
Проверим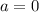 : имеем уравнение
: имеем уравнение 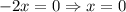 - очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
- очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
При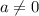 уравнение - квадратное вида
уравнение - квадратное вида 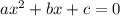 . Коэффициенты:
. Коэффициенты:  (внезапно),
(внезапно), 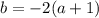 ,
,  . Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
. Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
Ищем дискриминант:
Найдем дискриминант трехчлена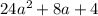 :
: 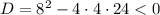
Это значит что при любых выражение
выражение 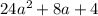
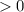 , т.е. исходное уравнение всегда имеет 2 корня.
, т.е. исходное уравнение всегда имеет 2 корня.
Могут быть три ситуации: 1) оба корня отрицательные; 2) корни имеют разные знаки; 3) оба корня положительные. Условию (нужно как минимум одно положительное решение) удовлетворяют только 2 и 3.
Проверим второй случай. Если корни имеют разные знаки, то достаточно условия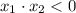 . По теореме Виета
. По теореме Виета 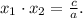 Так как в нашем случае
Так как в нашем случае 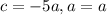 , то
, то 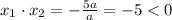 при любых
при любых  . Т.е. при любых значениях параметра (кроме
. Т.е. при любых значениях параметра (кроме 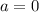 ) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
Значит, нас устраивают любые , кроме
, кроме 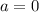 .
.
ОТВЕТ: при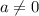 .
.