1. Алгебра
  2. При каких значениях параметра

При каких значениях параметра a сумма квадратов корней
уравнения x^2 −ax + a+ 1 = 0 равна 1?

vanyanazarenko1 vanyanazarenko1    2   29.06.2019 14:28    0

Ответы
егор1481 егор1481  23.07.2020 14:45

Существование корней:

D=a^2-4(a+1)=a^2-4a-40     (1)

По теореме Виета

x_1+x_2=a;\\ x_1x_2=a+1

x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=a^2-2\cdot(a+1)=1\\ \\ a^2-2a-2=1\\ \\ a^2-2a-3=0

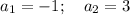
По теореме Виета a_1=-1;~~~ a_2=3

Подставим а = -1 и а = 3 в неравенство (1), имеем

(-1)^2+4+40 - верно

3^2-4\cdot3-40 - неверно.

ответ: при а = -1 сумма квадратов корней равна 1.

ПОКАЗАТЬ ОТВЕТЫ
ира967 ира967  23.07.2020 14:45

Решение задания приложено, добавлена проверка.


При каких значениях параметра a сумма квадратов корней уравнения x^2 −ax + a+ 1 = 0 равна 1?
При каких значениях параметра a сумма квадратов корней уравнения x^2 −ax + a+ 1 = 0 равна 1?
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
CasDavis CasDavis  10.10.2021 23:38
Выполни приведение подобных слагаемых....
guseva2yul guseva2yul  10.10.2021 23:38
Шустрый мышонок съедает головку сыра за 6 минут, а медленный — за 34. а) Какую часть одной головки сыра съедает шустрый мышонок за одну минуту? б) Какую часть одной головки...
valdi5p0ch22 valdi5p0ch22  10.10.2021 23:36
Галина Романовна раздала ученикам проверенные контрольные работы по теме Торжества . Маша получила 3 за 3 неверно выполненных задания...
haha1 haha1  10.10.2021 23:35
с промежутком знаковпостоянства , И можно с объяснением, учителю нужно с объяснением, иначе подумает что списал...
ahmedovadidi090 ahmedovadidi090  10.10.2021 23:35
Знайдіть значення виразу 8x^2y^4, якщо 2xy^2 = -5...
Ctatuetca Ctatuetca  10.10.2021 23:35
Чтобы построить график квадратичной функции, нужно: Расположите элементы в правильном порядке: 1через полученные точки провести параболу. 2составить таблицу значений с учетом...
rusnaktaniusha rusnaktaniusha  10.10.2021 23:32
Розв’яжіть нерівність, зобразіть множину її розв’язків на координатній прямій та запишіть цю множину у вигляді числового проміжку: ( ) а) x – 2 0; б) x + 3,5 ≥ 0; в) 5x ≥ 15;...
gireeva00 gireeva00  10.10.2021 23:32
2. В область определения функции, заданной формулой у входих число x - 4 не 2+ 1-2 2) 0 3) 4 4) 4 -2 3. Задайте формулой зависимость скорости движения о км/ч от времени t ч,...
Olgaekolesnik Olgaekolesnik  10.10.2021 23:26
Докажи, что значение выражения...
Gghfv Gghfv  05.05.2022 21:58
решить с 1 по 12 задания, расписать полностью решения....

Популярные вопросы