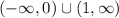При каких значениях параметра a любое решение неравенства х^2 - 3x + 2 < 0 будет решением неравенства ax^2 - (3a + 1)x + 3 < 0? !

x^2 - 3x + 2 = (x - 1)(x - 2) < 0

Решением этого неравенства является промежуток (1, 2)

Разложим на множители левую часть второго неравенства:

ax^2 - (3a + 1)x + 3 = (ax^2 - x) - (3ax - 3) = x(ax - 1) - 3(ax - 1) = (x - 3)(ax - 1) = a(x - 3)(x - 1/a)

Возможны 5 вариантов.

1) a > 1/3. Тогда решение неравенства – промежуток (1/a, 3). Нужно, чтобы промежуток (1, 2) полностью содержался в нём, так будет, если 1/a < 1. Объединяем с условием a > 1/3 и получаем часть ответа: a > 1.

2) a = 1/3. У второго неравенства нет решений.

3) 0 < a < 1/3. Решение неравенства – промежуток (3, 1/a); такой промежуток никогда не содержит (1, 2).

4) a = 0. Второе неравенство превращается в 3 - x < 0, x > 3. Не подходит.

5) a < 0. Решение второго неравенства – промежуток (1/a, 3), при этом 1/a < 0. Подходит.

ответ.