При каких значениях параметра a квадратное уравнение x^2+ax+a-1=0 имеет 1 корень?
Другие вопросы по теме Алгебра
Популярные вопросы
- Дан треугольник abc. bc=8, ac=9, угол c= 30 градусам. найдите площадь этого...
1 - Рулон ткани разрезали на две части длиной 6.3 м и 7.7 м.во сколько раз первая...
1 - Надо сочинение о природе кароткое . например бабочка , она была красивой...
2 - Много ! ! 5-7 примеров повторяющихся и схожих между собой событий в . конкретно...
3 - Составь программу действий и вычислить: (75-15)+(27-18-9)+26...
3 - Из села в город выехал мотоциклист со скоростью 53км/ч. в то же время из...
2 - Назовите идеологические течения, известные вам из курса .охарактеризуйте...
3 - Один автомат производит 6 тонн гвоздей за 12 часов. второй автомат 6 тонн...
1 - Прочитайте загадки. объясните отгадки. 1. летит орлица по синему небу, крылья...
1 - Мне нужен реферат на тему народы и страны (южной америки) на...
3
a=2, единственный корень x=-1
Объяснение:
При значении дискриминанта равного 0. Т.е.
a^2-4*(1)*(a-1)=0
a^2-4*a+4=0
Уже для этого уравнения дискриминант:
D = (-4)^2 - 4*1*4 = 16 - 16 = 0
a= 4/(2*1) = 2
Уравнение имеет единственный корень при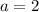
Теория:
Стандартный вид квадратного уравнения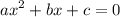
Его дискриминант равен
А его корни равны:
Объяснение:
Квадратное уравнение имеет один действительный корень тогда, когда его дискриминант равен нулю.
Для данного квадратного уравнения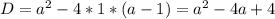
Получаем уравнение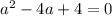 Это обычное квадратное равнение.
Это обычное квадратное равнение.
Решаем через дискриминант:
Данное квадратное уравнение имеет один действительный корень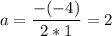
Значит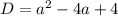 равна нулю при
равна нулю при 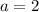
Следовательно уравнение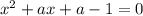 имеет один действительный корень при a = 2
имеет один действительный корень при a = 2