При каких значениях х имеет смысл выражения: log6(49-x^2) *** решить уравнение: 2^х=5; 7^2x+7^x-12=0

Ответы

666Лисица666 24.06.2020 22:07

Объяснение:

Так как логарифм определен на множестве положительных чисел, то выражение имеет смысл , если

$49-x^{2} 0;\\x^{2} -49<0;\\(x-7)(x+7)<0;\\-7<x<7.$

Значит выражение имеет смысл при x∈ ( -7; 7 ).

Решить уравнения

$2^{x} =5;\\2^{x} =2^{\log_25} ;\\x= \log_25.$

$7^{2x} +7^{x} -12=0;$

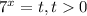Пусть $7^{x} =t, t0$ . Тогда уравнение принимает вид:

$t^{2} +t-12=0;\\D= 1+48=490\\\left [ \begin{array}{lcl} {{t=3,} \\ {t=-4.}} \end{array} \right.$

Так как t>0 , то t=3. Тогда

$7^{x} =3;\\7^{x} =7^{\log_73} ;\\x=\log_73.$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Алжсжсзвьвлвждчяь 10.12.2019 21:12

Сколько будет 3,8/0,1x+3 = 10/11 чему = x. , завтра к р 6 класс...

FireFox2017 10.12.2019 21:13

Построить график функции y = 2 в кубе...

Cat2081 10.12.2019 21:13

Ivanprofi22 10.12.2019 21:16

Жаман әдеттерден арылудың «плюс» түрі...

rortat32 10.12.2019 21:17

Ира21fu 10.12.2019 21:17

Log3(4x+3)=2 решить это уравнение...

UNDEADrevolution 10.12.2019 21:18

damiramirov321 18.02.2022 20:05

SlavaPereli 18.02.2022 19:58

Найти добуток многочленив (5-х) (5+х)...

Lukachyk2017 18.02.2022 19:48