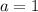При каких значениях а, система уравнений 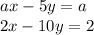
а) имеет единственное решение
б) не имеет решений
в) имеет бесконечное множество решений
Другие вопросы по теме Алгебра
Популярные вопросы
- Автобиографию А.С. Пушкина . Заранее ....
1 - Задание 1 Внимательно прочитайте текст о субъекте России и заполните...
3 - Имеются две хорошо отполированные пластинки алюминия и золота. Их кладут...
1 - Сочинение по цитате Жизнь показывает,что космос будут осваивать не...
1 - Укажите еденицы измерения плотности...
3 - В прямоугольной трапеции один из углов равен 78 градусов найдите углы...
1 - 0 , Знайдіть переріз числових проміжків (о;1) та (0,8; е). + (0,8:1)...
1 - Сойлемдерден омонимдерді тауып, қандай мағынада қолданылғанын корсетіндер...
2 - Першого дня прочитано 3/7 сторінок книги ,а другого дня решту 32ст....
2 - нужно обозначить орфограммы и вставить пропущенные буквы...
3
Разделим обе части второго уравнения на 2:
Решим систему уравнений методом подстановки. Выразим переменную из второго уравнения:
из второго уравнения:
Подставим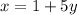 в первое уравнение системы:
в первое уравнение системы:
Решим данное уравнение в зависимости от значений параметра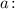
Если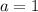 , то
, то 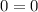 , значит,
, значит, 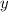 — любое число.
— любое число.
Если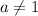 , то
, то 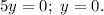 Тогда
Тогда 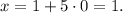
Система уравнений всегда имеет решения.
а)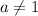
б)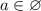
в)