При каких значениях а оба корня уравнения x2-(3a+2)x+8a-4a2=0 больше числа -7?
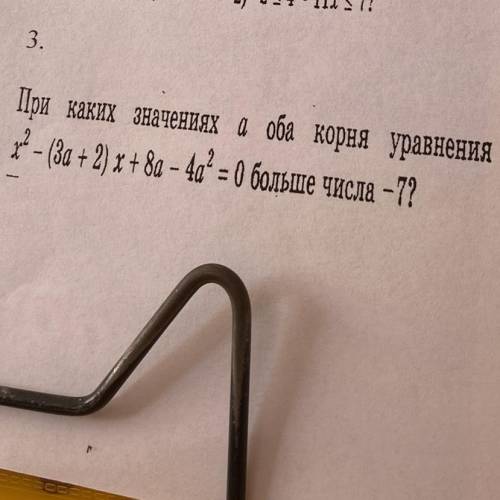
Другие вопросы по теме Алгебра
Популярные вопросы
- Прост о сколько будет 4 умножить на н минус м...
1 - Примеры прилагательных корень+н(суфф)+ый(окон) 15...
2 - 1)ивана и джулии об облаве: а-итальянец, который убежал с ними б-австрийский...
3 - вариант №3 1. используя график скорости определить: путь, пройденный...
3 - Найти пределы. вариант 4 а), б), в),г), д)...
2 - Таблица истинности символом f обозначено одно из указанных ниже логических...
1 - Куда возвращается использованная грязная вода? ...
2 - Расставьте нормативно-правовые акты в порядке увеличения их юридической...
3 - Вычислить: (125*64*27*8)^1/3 - (25*16*4)^1/2 +3 выберите один ответ:...
3 - Определите полный импульс поезда, состоящего из локомотива массой 300...
2
Найдём корни данного уравнения через дискриминант:
Данный дискриминант при любом значении а неотрицательный, а значит уравнение точно имеет 2 корня:
По условию, мы ищем такие значения параметра а, при которых оба корня больше -7, значит справедлива такая система: