При каких m уравнение (m - 3)x^2 - 6x + m + 5 = 0 имеет корни? Исследовать их знаки при различных m.

[ ]

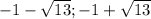Объяснение:

(m - 3)x² - 6x + m + 5 = 0

Имеет корни, если Д≥0.

Д=36-4*(m - 3)*(m + 5 )=-4m²-8m +96=-4(m²+2m-12).

-4<0 ⇒  (m²+2m-12)≤0 .

Корни  m²+2m-12=0  ,Д=4+48=52=4*13

х1=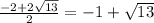

х2=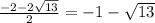

m²+2m-12≤0 , метод интервалов

+ + + + [ ]- - - - - - - { ]+ + + + + +

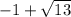х∈{ ]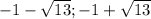

Исследуем  знаки корней  при различных m.

Если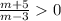 , то корни одинаковых знаков.По методу интервалов имеем + + + +(-5)- - - - -(3)+ + + + . Корни одинаковых знаков если m∈(-∞ ;-5)∪(3 ;+∞).

Если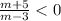 , то корни разных знаков.По методу интервалов имеем + + + +(-5)- - - - -(3)+ + + + . Корни разных знаков знаков если m∈(-5 ; 3 ).

Если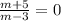 ,т.е m=-5  то уравнение x²+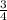*x=0  и корни 0 и -3\4.