Алгебра: При каких целочисленных значениях параметра a, система 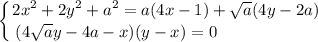имеет нечётное число решений.

При каких целочисленных значениях параметра a, система $\displaystyle \left \{ {{2x^2+2y^2+a^2=a(4x-1)+\sqrt{a}(4y-2a)} \atop {(4\sqrt{a}y-4a-x)(y-x)=0\qquad \qquad \qquad }} \right.$
имеет нечётное число решений.

Ответы

polina1347 27.12.2021 08:20

$\displaystyle \sf \left \{ {{2x^2+2y^2+a^2=a(4x-1)+\sqrt{a}(4y-2a)} \atop {(4\sqrt{a}y-4a-x)(y-x)=0}} \right.$

ОДЗ: a ≥ 0

Геометрия уравнений:

· 1-ое уравнение системы можно представить в виде

$\displaystyle \sf (x-a)^2+(y-\sqrt{a})^2=\frac{1}{2}(a-\sqrt{a})^2$

- это уравнение окружности с центром, движущимся по кривой y=√x и радиусом (a-√a)/√2.

· 2-ое уравнение - совокупность двух прямых

$\left[ \begin{gathered} \sf y =x \\ \sf \displaystyle y=\frac{x+4a}{4\sqrt{a}} \\ \end{gathered} \right$

1) Исследуем взаимное расположение первой прямой и окружности. Подставим y = x в первое уравнение системы. Получим квадратное уравнение:

$\sf \displaystyle 4x^2-4(a+\sqrt{a})x+(a+\sqrt{a})^2=0 \\ \frac{D}{4}=4(a+\sqrt{a})^2-4(a+\sqrt{a})^2=0$

⇒ прямая y = x является касательной к окружности при любых a ≥ 0, что дает нам одно решение системы:

$\sf \displaystyle x=y=\frac{a+\sqrt{a}}{2}$

(!) Заметим, что при a = 0 и a = 1 окружность вырождается в точку (0, 0) и (1, 1) соответственно ⇒ система имеет только одно решение при этих значениях a.

2) Исследуем взаимное расположение второй прямой и окружности. Подставим y = (x+4a)/(4√a) в первое уравнение системы. Получим квадратное уравнение:

$\sf \displaystyle \left(2+\frac{1}{8a}\right)x^2-4ax+a^2+2a\sqrt{a}-a=0 \\ \frac{D}{4}=4a^2-\left(2+\frac{1}{8a}\right)(a^2+2a\sqrt{a}-a)=2a^2-4a\sqrt{a}+\frac{15a}{8}-\frac{\sqrt{a}}{4}+\frac{1}{8}$

Оценим дискриминант при значениях a = 2, a = 3, a ≥ 4:

· a = 2

$\sf \displaystyle \frac{D}{4}=\frac{1}{8}(16\cdot 2^2-32\cdot 2\sqrt{2}+15\cdot 2-2\sqrt{2}+1)=\frac{1}{8}(95-66\sqrt{2})0$

т.к. 95/66 = (99 - 4)/66 = 1.5 - (2/33) > 1.5 - (7/100) = 1.43 > √2 ≈ 1.41

· a = 3

$\sf \displaystyle \frac{D}{4}=\frac{1}{8}(16\cdot 3^2-32\cdot 3\sqrt{3}+15\cdot 3-2\sqrt{3}+1)=\frac{1}{8}(190-98\sqrt{3})0$

т.к. 190/98 = (196-6)/98 = 2 - (6/98) > 2 - (7/100) = 1.93 > √3 ≈ 1.73

· a ≥ 4

$\sf \displaystyle \frac{D}{4}=2a^2-4a\sqrt{a}+\frac{15a}{8}-\frac{\sqrt{a}}{4}+\frac{1}{8}=\frac{1}{8}(16a^2-32a\sqrt{a}+15a-2\sqrt{a}+1)0$

- очевидно, т. к.

$\sf \displaystyle 16a^2+15a+132a\sqrt{a}+2\sqrt{a}$

ведь

$\sf \displaystyle 16a^2\geq 32a\sqrt{a} \\ 15a+1 2\sqrt{a}$

Таким образом, при целочисленном a ≥ 2 прямая пересекает окружность в двух различных точках и, соответственно, дает 2 решения системы. Убедимся что они не совпадают с полученным ранее решением при целочисленных a. Для этого подставим x = y = = (a + √a)/2 в уравнение y = (x + 4a)/(4√a), откуда найдем a = (33+5√41)/32 - не явл. целочисленным.

При a = 0 и a = 1 система имеет одно решение. При a ≥ 2, a ∈ Z система имеет 3 решения.

ответ: при любых целочисленных a ≥ 0.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра