При каких "a" уравнение имеет решение? 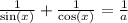
Другие вопросы по теме Алгебра
Популярные вопросы
- Приложение из этих слов , you, hand? What ,dolding,in,are ,you , your...
2 - Словообразования на слово разноцветный...
3 - 1) При яких значеннях виразу (2y+3)/4 належить проміжку [-2; 4] ? 2)...
2 - Describing animals. Повторение Put the adjectives in the box in the...
2 - Ищу друзей заявки кидайте мне...
1 - Write a short story about famous artists of Ukraine (10-15 sentences)...
3 - плз, только подробно надо Даны вершины треугольника А(-3; -1), В(5;...
3 - Первый автомобиль едет со скоростью 54 км/ч, а второй со скоростью...
1 - 2. Соотнеси кеннинги и их значения. Луны лба Влага чаек Море ран Кряж...
2 - Военной школа, которую закончил поэт....
1
Рассмотрим интервал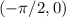 . На нем функция
. На нем функция  непрерывна. Более того, при
непрерывна. Более того, при 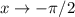 функция
функция 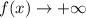 , а при
, а при 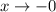 функция
функция 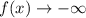 . Тогда можно выбрать такие точки
. Тогда можно выбрать такие точки  и
и 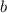 из соответственно правой и левой полуокрестностей
из соответственно правой и левой полуокрестностей 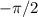 и
и 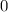 , что для заданного наперед
, что для заданного наперед 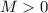 будет верно, что
будет верно, что 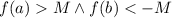 . А тогда можно применить теорему Больцано-Коши (о промежуточном значении) для отрезка
. А тогда можно применить теорему Больцано-Коши (о промежуточном значении) для отрезка ![[a,b]\subset (-\pi/2,0)](/tpl/images/4742/8553/1968d.png) и получить, что
и получить, что 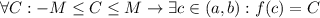 . Тогда область значений
. Тогда область значений 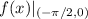 есть
есть 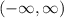 , то есть уравнение имеет решение при всех
, то есть уравнение имеет решение при всех 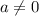 .
.