преобразовать алгебраическую дробь в выражение .
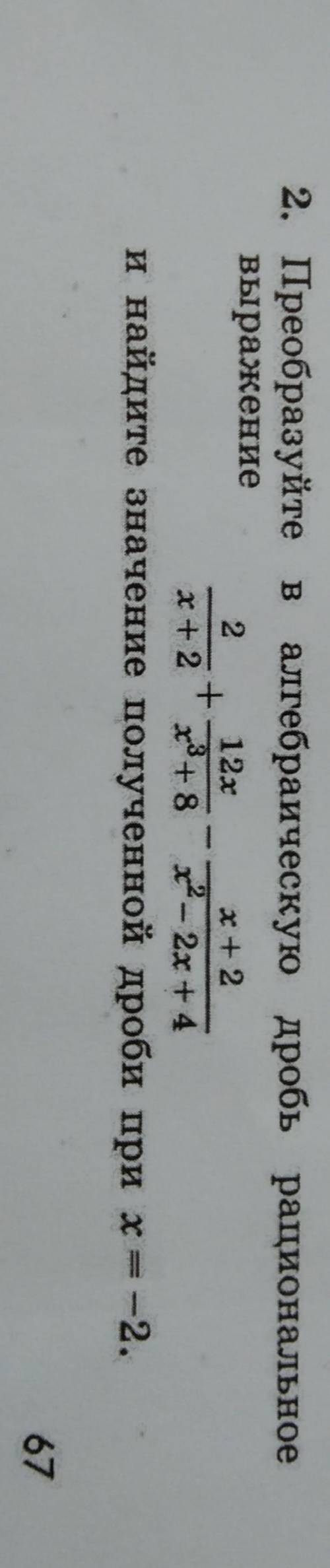
Другие вопросы по теме Алгебра
Популярные вопросы
- Выбегая из леса саша увидел стадо оленей которое медленно передвигались...
3 - Термі! головний герой пісні марусі чурай,,засвіт встали...
3 - 84: 7= 84: 7умножить на 5= 84-84: 7 умножить на 5=...
2 - Наведіть два приклади рівнянь реакцій утворення кальцій етаноату...
1 - Покоящеяся тело начинает движение с постоянным ускорением. в третью секунду...
1 - Вуниверситетскую библиотеку новые учебники по для 1-3 курсов, по 240 штук...
1 - Какому одночлену равняется выражение 4х²у³*0,5ху²?...
2 - 1)al2o3+hcl=alcl3+h2o. al2o3+naoh=na2alo2+h2o. 2)al(oh)3+hcl=alcl3+h2o....
2 - На 100 грамм мяса надо взять 60 грамм свеклы. сколько надо грамм свеклы...
3 - Fahrrad fahren выберите один ответ: 1)hast 2)magst 3)machst...
1
1) После преобразования получена дробь:
2) Значение полученной дроби при х = -2 равно нулю.
Объяснение:
Если заметить, что 8 = 2³, а 4 = 2², то напрашивается использование формулы суммы кубов:
для приведения всех дробей к единому знаменателю.
Домножим у каждой дроби числитель и знаменатель на недостающие множители:
После сокращения мы получаем вполне "красивую" дробь:
Однако - стоит отметить, что строго говоря, данная дробь не равносильна исходной.
При сокращении мы убрали из знаменателя множитель (х+2), поэтому, несмотря на то, что полученное в конце выражение при х=-2 имеет вполне конкретное и определенное значение,
(!) при х = -2 исходное выражение не определено, что обязательно нужно указать и учитывать при сокращении дробей!
Однако нас просят найти значение полученной дроби, что вполне реально. Итак:
при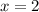 значение выражения
значение выражения 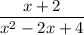 равно:
равно:
Итак, ответ:
1) После преобразования получена дробь:
2) Значение полученной дроби при х = -2 равно нулю.