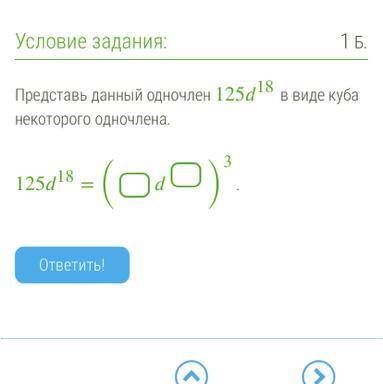
Представь данный одночлен 125d18 в виде куба некоторогоодночлена

0,125d¹⁸ = (0,5d⁶)³

Объяснение:

так как 0,5³ = 0,125 , а (d⁶)³ = d⁶ˣ³ =d¹⁸

Чтобы представить данный одночлен 125d^18 в виде куба некоторого одночлена, мы должны найти корень кубический из этого одночлена. Для этого, мы найдем корень кубический из коэффициента и корень кубический из переменной.

1. Коэффициент 125 - это 5^3, так как 5 * 5 * 5 = 125. Значит, мы можем вынести 5 за скобку и оставить 25d^18.

2. Теперь посмотрим на переменную d. Чтобы найти корень кубический из d^18, мы должны поделить показатель степени на 3. В данном случае, 18/3 = 6. Значит, мы можем вынести d^6 из под корня и оставить d^6 за скобку.

Итак, мы представляем данный одночлен 125d^18 в виде куба некоторого одночлена как (5d^6)^3. Это означает, что мы возведем 5d^6 в куб и получим 125d^18.