Предлагается любителям сложных заданий:))

Пусть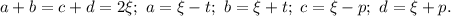

Пусть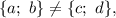 тогда t≠±p; не уменьшая общности, можно считать, что 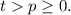Пусть n=2k+1. Используя бином Ньютона, можем написать

Это выражение может равняться нулю только если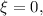 а это и означает, что a=-b; c=-d. Утверждение доказано.

если 2 множества не равны, то в 1 множестве есть элемент который больше других элементов другого множества. Покажем, что нам выгодно увеличивать 1 элемент множества, чтобы увеличить его сумму в степени n: докажем это.

скажем что a > b

(a ^ n) + b ^ n < (a + 1) ^ n + (b - 1) ^ n

это можно увидеть раскрыв скобки и приведя подобные

следовательно если 2 множества различны или не равны 0 система не выполняется