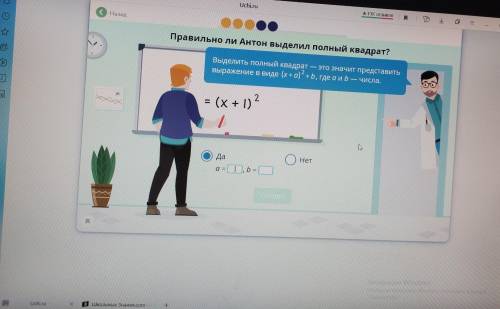
Правильно ли Антон выделил полный квадрат?

да

Объяснение:

Выведение полного квадрата- это такое тождественное преобразование, при котором заданный трёхчлен представляется ввиде (а+b)2

суммы или разности квадрата двухчлена и некоторого числового или буквенного выражения, все верно.

Чтобы определить, правильно ли Антон выделил полный квадрат, нам необходимо знать определение полного квадрата. Полным квадратом называется квадратный трехчлен, который представляет собой квадрат двучлена.

Для определения, правильно ли Антон выделил полный квадрат, мы можем разложить выражение на сомножители или возвести его в квадрат.

Данное выражение: x^2 + 4x + 4

Для проверки, давайте разложим его на сомножители:

x^2 + 4x + 4 = (x + 2)(x + 2)

Как мы видим, мы получили два одинаковых множителя (x + 2). Это означает, что выражение действительно является полным квадратом.

Если мы хотим получить квадрат двучлена, мы можем возвести x + 2 в квадрат:

(x + 2)^2 = (x + 2)(x + 2) = x^2 + 2x + 2x + 4 = x^2 + 4x + 4

Как видите, мы получили исходное выражение x^2 + 4x + 4, что подтверждает, что оно является полным квадратом.

В заключение, мы можем сказать, что Антон правильно выделил полный квадрат, так как выражение x^2 + 4x + 4 представляет собой квадрат двучлена (x + 2)^2.