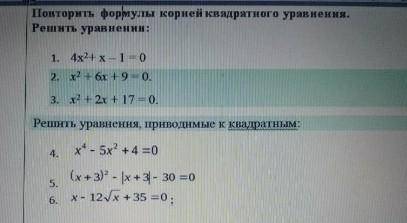
Повторить формулы корней квадратного уравнения. Решить уравнения
Решение по возможности обязательно​

ответ: x1=3, x2=-9.

Объяснение:

(x+3)²-/x+3/-30=0. Так как /x+3/=√(x+3)², то, полагая x+3=t, получаем уравнение относительно t: t²-√t²-30=0. Отсюда √t²=t²-30, и, возводя обе части в квадрат, приходим к уравнению t⁴-61*t²+900=0. Полагая теперь u=t², получаем уравнение u²-61*u+900=0. Его дискриминант D=61²-481*900=121=11², поэтому оно имеет корни u1=(61+11)/2=36 и u2=(61-11)/2=25. Из уравнения t²=36 находим t1=6, t2=-6. Из уравнения t²=25 находим t3=5, t4=-5. Отсюда x1=t1-3=3, x2=t2-3=-9, x3=t3-3=2, x4=t4-3=-8. Подставляя найденные корни в исходное уравнение, убеждаемся, что корни x3 и x4 - посторонние. Поэтому уравнение имеет два корня: x1=3, x2=-9.