Потрібне детальне пояснення (із прикладами) теми 9 класу з алгебри: "Основні властивості числових нерівностей".
Другие вопросы по теме Алгебра
Популярные вопросы
- Выберите пункт, который не входит в технологический этап. Укажите...
2 - Пропорцияның белгісіз мүшесін тап -3,45/2,1=1/15/-х помагите пожолуйста...
2 - «Астана ЭКСПО-2017» халықаралық мамандандырылған көрмесі – тәуелсіз...
2 - 2. Этилен взаимодействует с каждым из пары веществ, форму- лы...
2 - Запиши число обротное данному 25/63...
2 - Я пам ятаю мить чудову (враження)...
3 - Вопросы по тексту К. Станюковича «Рождественская ночь» 1.Где происходило...
3 - Составьте схему источников загрязнения воздуха...
3 - Знайти середню лінію рвностороннього трикутника периметр якого...
3 - 2. Дано: AB = 26 , BC = корень235Найти: AC....
3
Здравствуйте!
1. Если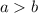 и
и 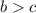 , то
, то 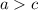
Простым языком: Если первое число больше второго, а второе- больше третьего, то первое число всегда больше третьего. Это логично, ведь получается, что первое число будет самым большим из перечисленных.
Обратно: Если и
и 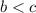 , то
, то 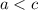
Примеры:
7>4, 4>1, поэтому 7>1.
5> -3, -3> -6, поэтому 5> -6
10<15, 15<30, поэтому 10<30.
2. Если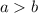 , то
, то 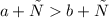
Простым языком: если увеличить обе части неравенства на любое число, то неравенство останется прежним.
Обратно: Если , то
, то 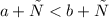
Примечание: с может быть отрицательным числом, поэтому также справедливо неравенство: Если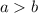 , то
, то 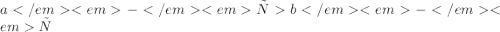
Примеры:
5>2, поэтому 5+1>2+1 (6>3)
5>2, поэтому 5-2>2-2 (3>0)
6<20, поэтому 6+10<20+10 (16<30)
6<20, поэтому 6-4<20-4 (2<16)
3. Если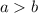 и m>0, то
и m>0, то 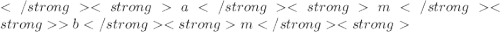
Простым языком: если умножить каждую часть неравенства на положительное число, то неравенство останется прежним.
Обратно: Если и m>0, то
и m>0, то 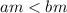
Примеры:
9>4, поэтому 9*5>4*5 (45>20)
8<16, поэтому 8*3<16*3 (24<58)
4. Если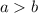 и m<0, то
и m<0, то 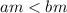
Простым языком: если умножить каждую часть неравенства на отрицательное число, то знак неравенства поменяется.
Обратно: Если и m<0, то
и m<0, то 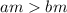
Примеры:
9>4, поэтому 9*(-5)>4*(-5) (-45<-20)
-5<-1, поэтому (-5)*(-3)<(-1)*(-3) (15>3)
5. Вытекает из 4-го: Если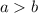 , то
, то 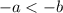
Простым языком: если умножить каждую часть неравенства на (-1), то знак неравенства поменяется.
Обратно: Если , то
, то 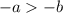
Примеры:
9>4, поэтому -9<-4
-5<-1, поэтому 5>1
6. Если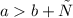 , то
, то 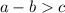
Простым языком: если перенести число из одной части неравенства в другую, то число поменяет свой знак, а знак неравенства останется прежним.
Обратно: Если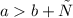 , то
, то 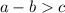
Примечание: с может быть отрицательным числом, поэтому также справедливо неравенство: Если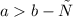 , то
, то 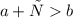
Примеры:
7>2+3, поэтому 7-3>2
8>7-1, поэтому 8+1>7
Все эти свойства были приведены к строгим неравенствам. У нестрогих неравенств свойства точно такие же, только они имеют знак "не больше" или "не меньше".
Краткие свойства нестрогих неравенств:
1. Если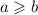 и
и 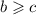 , то
, то 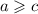
2. Если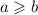 , то
, то 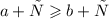
3. Если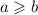 и m>0, то
и m>0, то ![am \geqslant bm[/tex]4. Если [tex]a \geqslant b](/tpl/images/3827/0725/f79c1.png) и m<0, то
и m<0, то 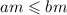
5. Если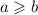 , то
, то 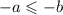
6. Если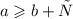 , то
, то