Постройте график функции y=5x^2-10x-40/(x^2+2x)(4-x) и определите при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
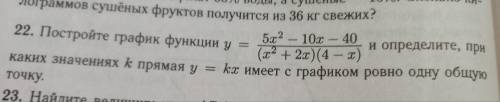
Другие вопросы по теме Алгебра
Популярные вопросы
- Шалопаи били стекла. шалопаев били стекла. определить главное слово в предложении...
2 - Найти по 2 примера именных, глагольных, наречных словосочетаний можно выделить...
1 - Сделать морфологический разбор слов: твоими, скромен, доставит, своими...
1 - Если масштаб 1: 10 000, а расстояние на карте равно 35,5см, как определить...
3 - Найдите значение выражения a3+b3,если a+b=3 и ab=5. а)-18 б)19 в)9 г)-12...
2 - 308 и 585 являются ли эти числа взаимно простыми ? и разложите мне их ато...
3 - Проведите примеры что в европе в xvi в происходила конная революция...
1 - Решить . в 0 часов 00 мин началась посадка на поезд.в 0 часов 30 мин поезд...
3 - Найти вес сообщения осенью идут дожди...
3 - Что люди делают чтобы изучить - скажите на с переводом...
2
Объяснение:
Требуется построить график функции и определите при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
1.
Разложим числитель на множители. В знаменателе вынесем х из первой скобки:
Далее вынесем минус и сократим дробь. Не забываем про область определения функции:
Dy: x ≠ 0; x ≠ -2; x ≠ 4;
или х ∈ (-∞;-2) ∪ (-2;0) ∪ (0;+∞)
2. Строим график - гипербола, расположена во 2 и 4 четвертях.
Возьмем точки:
х=1; y=-5;
x=2; y=-2,5;
x=5; y=-1
Вторую ветвь гиперболы строим симметрично начала координат.
Отметим "выколотые" точки.
x ≠ -2; x ≠ 4
3. При каких значениях k прямая y=kx имеет одну общую точку?
Прямая проходит через начало координат.
Эти прямые пройдут через "выколотые" точки.
Подставим их координаты в уравнение прямой и найдем k:
1) (-2; 2,5)
2,5=k*(-2)
k = -1,25 ⇒ y = -1,25x
2) (4; -1,25)
-1,25=k*(4)
k = - 0,3125 ⇒ y = -0,3125x