Построить график функции у при х> 0, если у=х²-х. достроить график функции для х< 0 так, чтобы построенная линия была графиком: а) четной функции; б) нечетной функции. задать формулой каждую из полученных функций. не надо строить, если как найти формулы только? ?

а) раз четная, значит одинаковые значения как для х, так и -х, значит графичек у=х²-|х|, то есть линия симметричная изначальной относительно ОУ

б)нечетная это такая же линия только направленная вниз, и формула будет: у=-х²+х

1) Для четной функции необходимо чтобы выполнялось равенство f(x)=f(-x)

Для части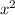  оно выполняется для x будетвыполнятся если поставить модуль

Формула  

2) Для нечетной функции необходимо чтобы выполнялось равенство f(-x)=-f(x)

Формула

Графики во вложении